1 / 1

Aufgabenstellung:

Es seien und wegzusammenhängende topologische Räume mit jeweils mehr als einem Punkt. Es sei . Zeige, dass der Raum wegzusammenhängend ist.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

Betrachte zwei beliebige Punkte und in . Wir wollen einen Weg zwischen diesen beiden Punkten finden.

Da und wegzusammenhängend sind, gibt es Wege von nach und von nach .

Im Allgemeinen kann man nicht den Weg benutzen, da auf diesem Weg liegen könnte!

Stattdessen müssen wir eine Fallunterscheidung machen:

  1. Falls und , nehme .
  2. Falls und , nehme .
  3. Falls : Es kann nicht eintreten, sonst wäre . Also tritt entweder Fall 2 ein, oder . In letzterem Fall nutzen wir, dass mindestens zwei Punkte hat, und wählen einen Hilfspunkt , sowie einen Weg von nach . Nun nehme .
  4. Falls : analog zu Fall 3.

Zur Veranschaulichung: Eine bildliche Darstellung der Fälle 1 bis 3 für , :

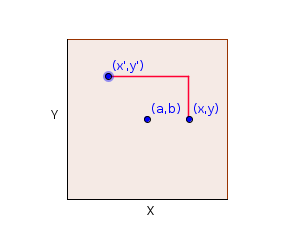
Ein Quadrat mit Mittelpunkt (a,b). (x,y) liegt rechts von (a,b), (x',y') liegt links oberhalb. Der eingezeichnete Pfad führt von (x,y) zuerst senkrecht nach oben und dann nach links zu (x',y').

Ein Quadrat mit Mittelpunkt (a,b). (x,y) liegt unterhalb von (a,b), (x',y') liegt links oberhalb. Der eingezeichnete Weg geht zuerst von (x,y) nach links und dann nach oben zu (x',y').

Ein Quadrat mit Mittelpunkt (a,b). Unterhalb von (a,b) liegt (x,y), oberhalb liegt (x',y'), und rechts liegt (c,b). Der eingezeichnete Weg führt von (x,y) über (c,b) nach (x',y').

Lösung:

Durch eine Fallunterscheidung kann für zwei beliebige Punkte in ein verbindender Weg angegeben werden.