Aufgabenstellung:
Die im Bild dargestellte Schaltung enthält eine Spule mit der Induktivität
Es ist der zeitliche Verlauf des Stromes
Schaltvorgang in einem ohmsch-induktiven Stromkreis:
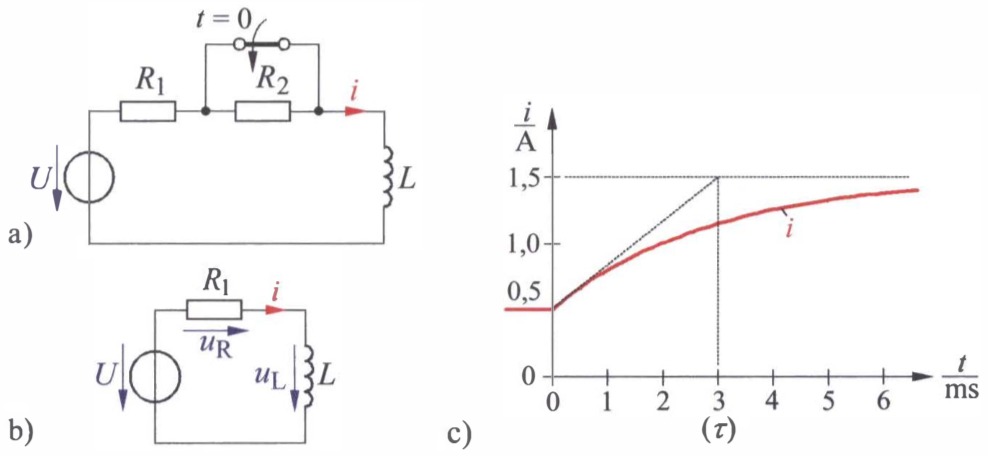
a) Gegebene Schaltung, b) vorliegende Schaltung nach dem Einschalten des Schalters, c) zeitlicher Verlauf des im Kreis fließenden Stromes
Lösungsweg:
Durch das Schließen des Schalters entsteht die in Bild b dargestellte Schaltung. Darin ist
Mit
Es entsteht also eine Differenzialgleichung. Zu deren Lösung zerlegen wir den gesuchten Strom in
Hierbei sei
Da der Strom
Durch Subtrahieren ergibt sich:
Wir erhalten also zur Bestimmung der Ströme
Den stationären Strom
Der Strom beträgt daher
Zur Ermittlung des freien Stromes
Daraus wird durch Integrieren, wenn wir den im Zeitpunkt
Durch Ausführen der Integration und Einsetzen der Grenzen finden wir
Daraus folgt, wenn wir
Damit haben wir die Lösung für den Verlauf des freien Stromes
Ergebnisse einsetzen bringt:
Zur Bestimmung der hierin enthaltenen Konstanten
Sie besteht im vorliegenden Fall darin, dass im Zeitpunkt
auftritt. Setzen wir diese Anfangsbedingung ein, so ergibt sich
Hieraus folgt, wenn wir berücksichtigen, dass
Wir setzen dieses Ergebnis ein und erhalten so als Lösung für den gesuchten Strom
In Bild c ist der zeitliche Verlauf dargestellt. Der Strom