1 / 1

Aufgabenstellung:

In der Schaltung nach Bild a soll ein Kondensator mit der Kapazität über eine Spule mit der Induktivität und einen Wirkwiderstand von mit einer Wechselspannungsquelle verbunden werden. Diese liefert eine (sinusförmige) Spannung mit dem Scheitelwert und der Frequenz . Der vorhandene Schalter wird im positiven Scheitelwert der Spannung geschlossen.

Es ist der zeitliche Verlauf der Kondensatorspannung zu ermitteln und grafisch darzustellen.

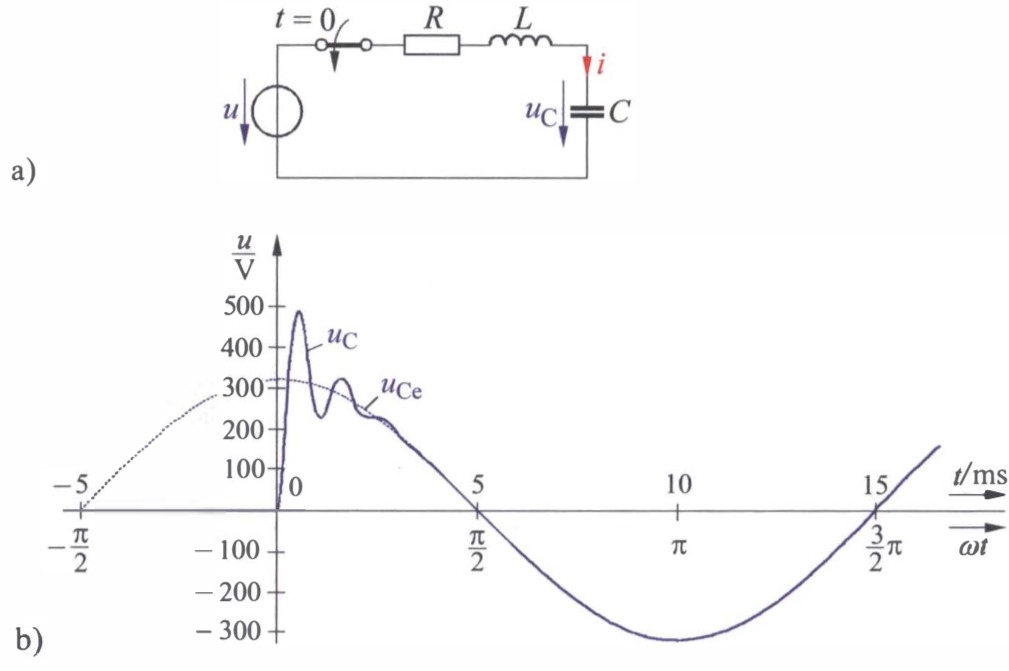
Abbildung

a) Gegebene Schaltung,
b) zeitlicher Verlauf der Kondensatorspannung

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

Kondensatorspannung

Wir führen der folgenden Abbildung die Teilspannungen und sowie den Strom ein.

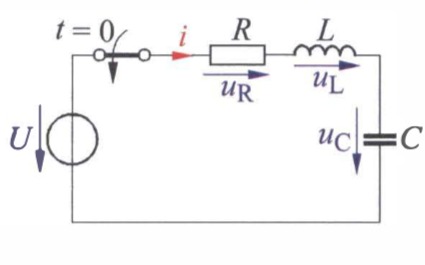
Abbildung

In der Schaltung gilt

Mit

wird aus Gl. (1)

Die Differenzialgleichung zur Bestimmung von lautet:

Hierbei können wir die anliegende Wechselspannung durch

darstellen.

Da der Schalter im positiven Scheitelwert der Spannung geschlossen wird, ist Aus Gl. (14.87) wird deshalb

Zur Lösung dieser Differenzialgleichung wählen wir den Ansatz

Für den Scheitelwert der stationären Kondensatorspannung gilt nach der Spannungsteilerregel (Bild a)

Mit

und

wird

Die Spannung ist in Bild 14.13a gegenüber dem fließende Strom um

phasenverschoben. Da gegenüber wiederum um nacheilt, erhalten wir für den zeitlichen Verlauf der stationären Kondensatorspannung (unter Beachtung von Gl. (3) mit )

Für die freie Kondensatorspannung lautet die allgemeine Lösung

Hierbei betragen die Konstanten und

Wir erhalten also konjugiert komplexe Ergebnisse. Diese wollen wir nachfolgend durch

darstellen, wobei ist und .

Setzen wir Gl. (5) in Gl. (4) ein, so können wir die sich ergebende Gleichung umformen in

Dabei sind und noch zu bestimmende Konstanten. Aus der Gleichung ist ersichtlich, dass Schwingungen auftreten. Man spricht daher auch vom periodischen Fall.

Wir setzen die in den Gl. (6) und (7) dargestellten Ergebnisse in Gl. (8) ein und erhalten mit die allgemeine Lösung für die Kondensatorspannung als

Die hierin enthaltenen Konstanten und bestimmen wir aus den Anfangsbedingungen. So ist im Zeitpunkt bei einem ungeladenen Kondensator ebenfalls . Setzen wir diese Bedingung in Gl. (4) ein, so ergibt sich

Hieraus folgt

Weiterhin muss im Zeitpunkt auch sein, weil die Spule eine sprunghafte Stromänderung nicht zulässt. Folglich muss wegen im Zeitpunkt ebenfalls sein. Wir differenzieren daher Gl. (4) nach und erhalten

Setzen wir hierin die Bedingung für ein, so ergibt sich, wenn wir die sich ergebende Gleichung nach auflösen,

Setzen wir die ermittelten Werte in Gl. (4) ein, so erhalten wir

Mit

und

können wir den gesuchten Verlauf der Kondensatorspannung auch angeben durch

In Bild b ist dieser Verlauf grafisch dargestellt. Dabei ist der stationären Kondensatorspannung mit der Kreisfrequenz

und der Periodendauer

die nach einer e-Funktion abklingende freie Kondensatorspannung überlagert. Sie hat die Kreisfrequenz die Periodendauer

und klingt mit der Zeitkonstanten

ab.

Lösung: