3 / 3

Aufgabenstellung:

In der folgenden Skizze finden Sie das Weg-Zeit-Diagramm für eine ungedämpfte harmonische Bewegung.

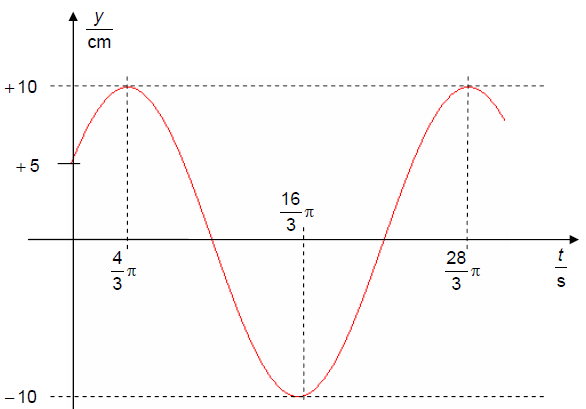
new alt text

  1. Bestimmen Sie aus diesem Diagramm und den angegebenen Daten
    (a1) die Amplitude ,
    (a2) die Schwingungsdauer ,
    (a3) die Eigenfrequenz ,
    (a4) die Eigenkreisfrequenz ,
    (a5) den Nullphasenwinkel .

  2. Stellen Sie die Bewegungsgleichung für die gezeichnete ungedämpfte harmonische Schwingung auf.

  3. Berechnen Sie die Geschwindigkeit für den Zeitpunkt .

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Bestimmung der Konstanten:

Werte aus dem Diagramm ablesen:

Amplitude:

Schwingungsdauer:

Daraus ergeben sich die Werte für die Frequenz und Kreisfrequenz:

Somit gilt für :

Der Wert des Nullphasenwinkels hängt davon ab, ob für die Beschreibung der Kurve eine Kosinus- oder eine Sinus-Funktion gewählt wird. Hier wird der Ansatz mit der Kosinus-Funktion zugrunde gelegt.

Berechnung des Nullphasenwinkels

Der Kosinus-Ansatz für das Weg-Zeit-Gesetz liefert für mit dem aus dem Diagramm abgelesenen Wert . Aus folgt mit dem abgelesenen Wert

und somit ist im Bogenmaß

Für den gewählten Cosinus-Ansatz ist die Auslenkung nacheilend, d. h. nur das negative Vorzeichen kommt in Frage (das erste Maximum der Kurve liegt nicht bei , sondern bei , also zeitlich später).

Ein kürzerer Lösungsweg:

Das erste Maximum liegt bei .

Damit ergibt sich

b) Bewegungsgleichung  

Der Kosinus-Ansatz führt somit auf

Hinweis:

Hätte man einen Sinus-Ansatz gemacht, so hätte sich als Beschreibung des Diagramms ergeben

Für einen Sinus-Ansatz ist die Auslenkung gegen eine Standard-Sinus-Funtkion voreilend.

(c)  Berechnnung der Geschwindigkeit für den Zeitpunkt

Die Geschwindigkeit erhält man durch Ableiten des Weg-Zeit-Gesetzes nach der Zeit

Für die vorliegende Schwingung wird für

Lösung:

  1. Amplitude

    Schwingungsdauer

    Frequenz

    Kreisfrequenz

    Auslenkungen

    Nullphasenwinkel für Kosinus-Ansatz: Auslenkung nacheilend negatives Vorzeichen

  2. Kosinus-Ansatz liefert

  3. Geschwindigkeit