Aufgabenstellung:
Berechne den Flächeninhalt eines Kreises mit dem Radius
Fertige eine Skizze an und rechne jeweils:
1. mit kartesischen Koordinaten
2. mit Polarkoordinaten
Die Aufgabe soll verdeutlichen, welchen Vorteil Polarkoordinaten gegenüber kartesischen Koordinaten haben können.
Lösungsweg:
Fertige eine Skizze an und trage die zur Berechnung relevanten Größen und Funktionen ein:
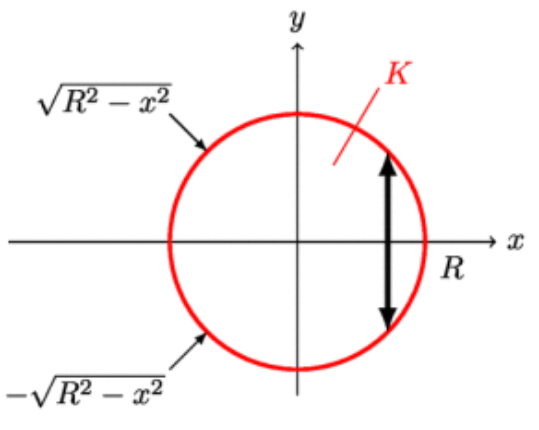
1. Lösung über kartesische Koordinaten:
Schreibe die Gleichung des Kreises so um, das du sie als Integralgrenzen nutzen kannst. (Nominalbereich)
Bilde das zu lösende Doppelintegral mit angetragenen Integralgrenzen:
Löse das Integral von innen nach außen:
Löse weiter über eine geeignete Substitution:
Es gilt für die Substitution:
Und somit weiter für das Integral:
Nutze das Additionstheorem
2. Lösung über kartesichen Koordinaten:
Führe Polarkoordinten
Löse das umgeschriebene Integral: