Aufgabenstellung:
Die folgende Verstärkerschaltung wird mit einem Operationsverstärker
Für den Operationsverstärker gilt:
- Ermitteln Sie die Ausgangsspannung
als Funktion der Eingangsspannungen und der Widerstände bis . Verwenden Sie das Superpositionsprinzip. - Geben Sie die Spannung
mit den Zahlenwerten an, die Ihnen zur Verfügung stehen.
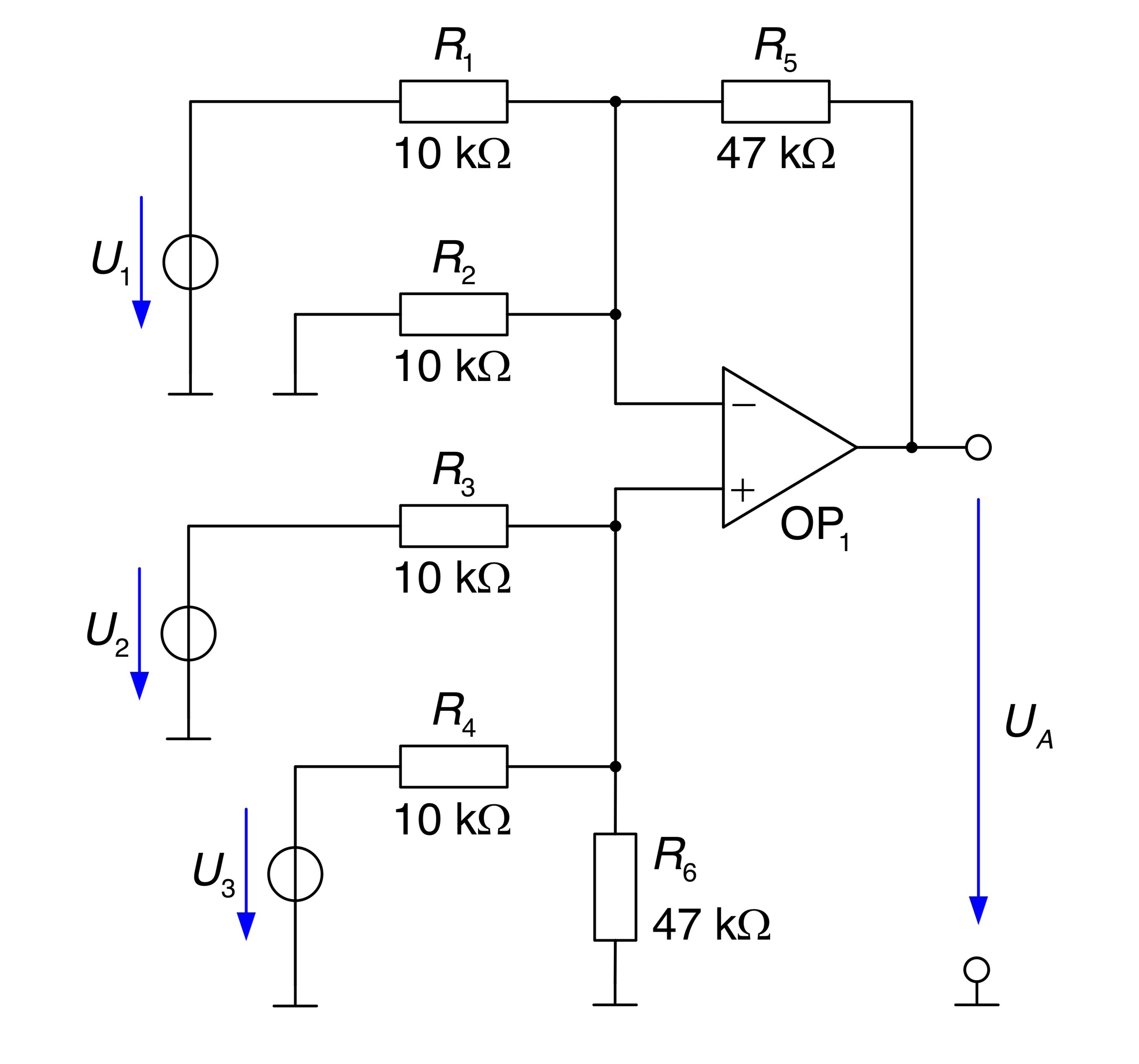
Lösungsweg:
a) Allgemeines Bestimmen der Ausgangsspannung
Die Berechnung der Ausgangsspannung erfolgt nach dem Superpositionsprinzip.
Zunächst werden die Spannungsquellen
Durch die Widerstände
Es ergibt sich die Schaltung eines invertierenden Verstärkers.
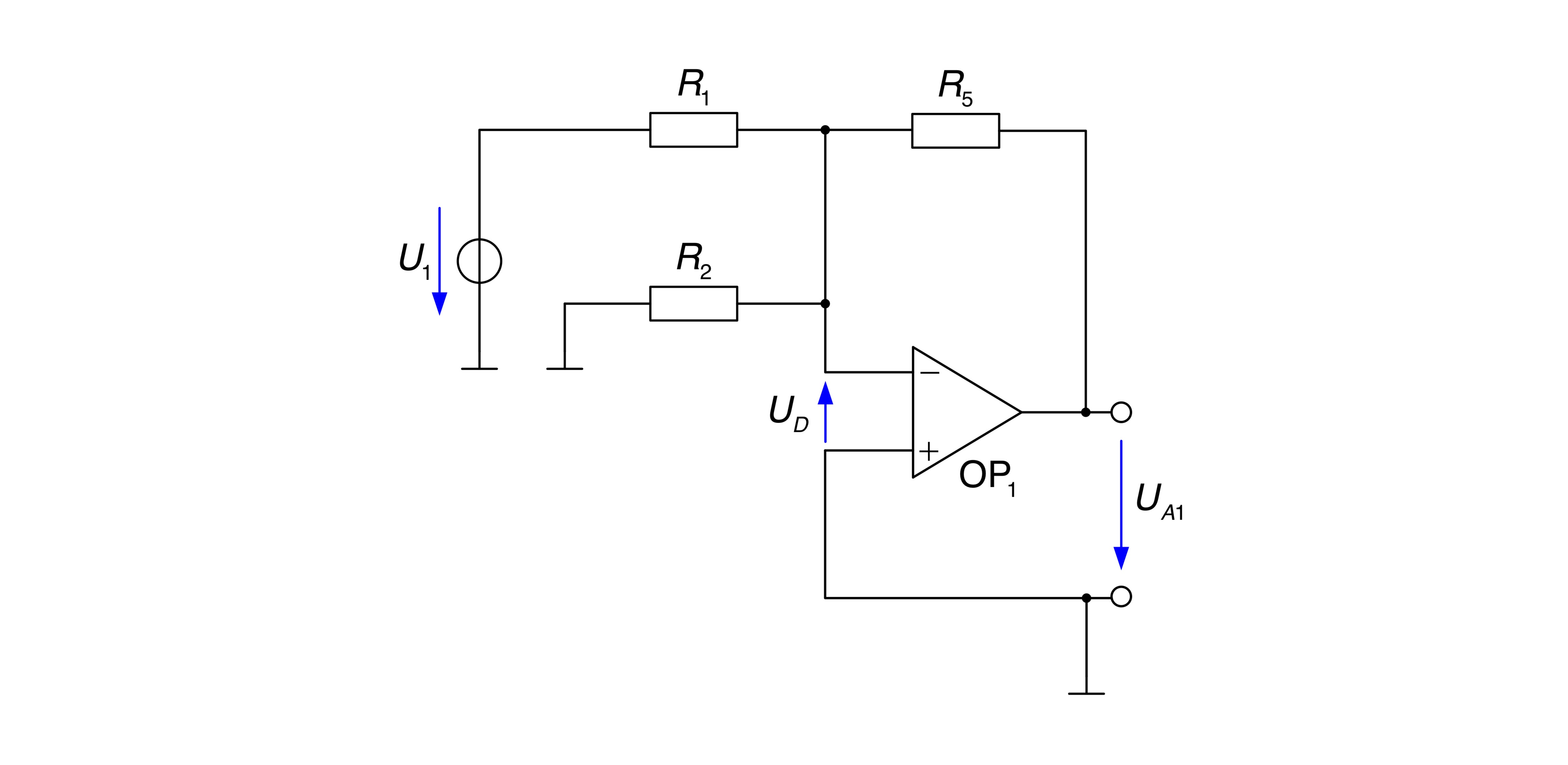
Ebenso fließt durch den Widerstand
Im nächsten Schritt könnte das Superpositionsprinzip weiter angewendet werden, in dem die Spannungsquellen
An dieser Stelle soll allerdings ein Zwischenschritt angewendet werden, in dem lediglich die Spannungsquelle
Aus diesen Spannungsquellen und den Widerständen
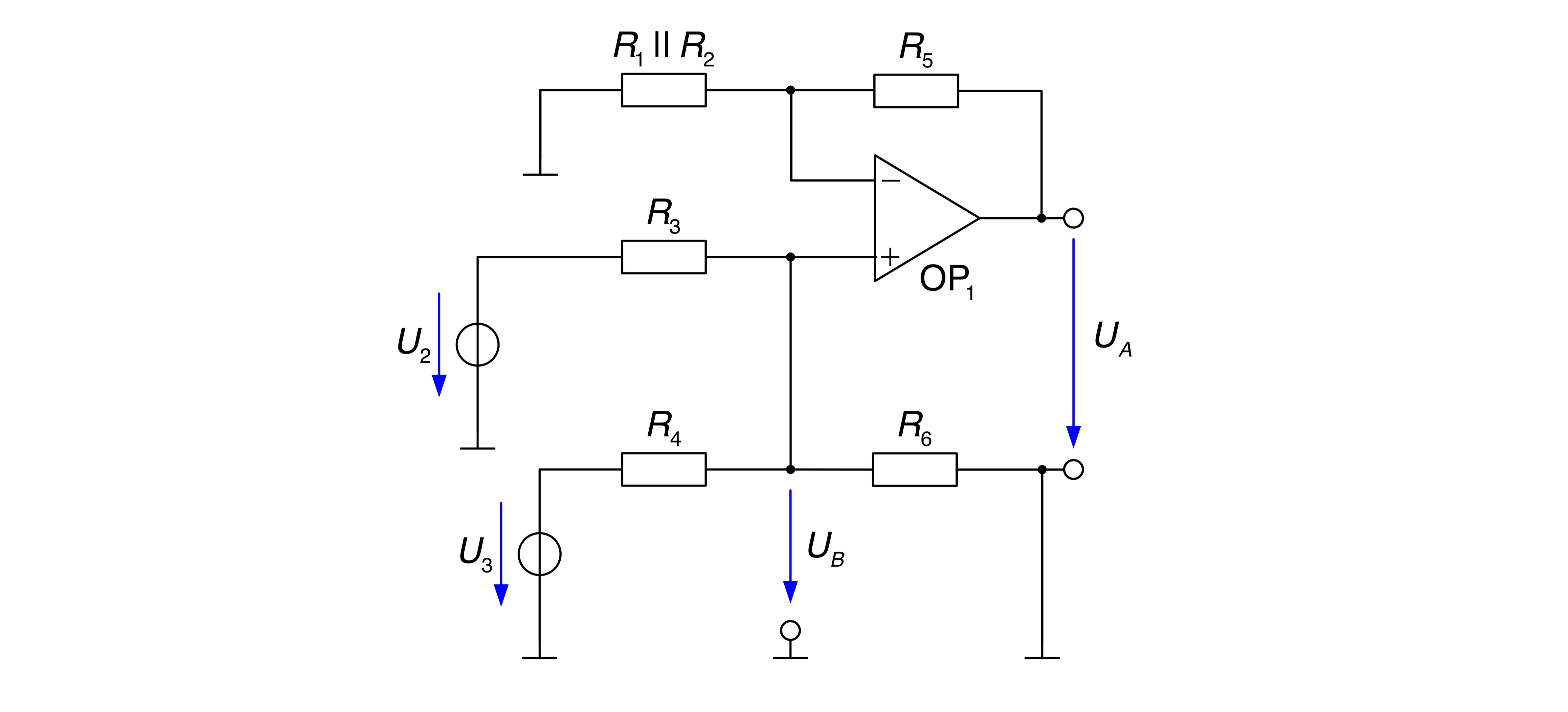
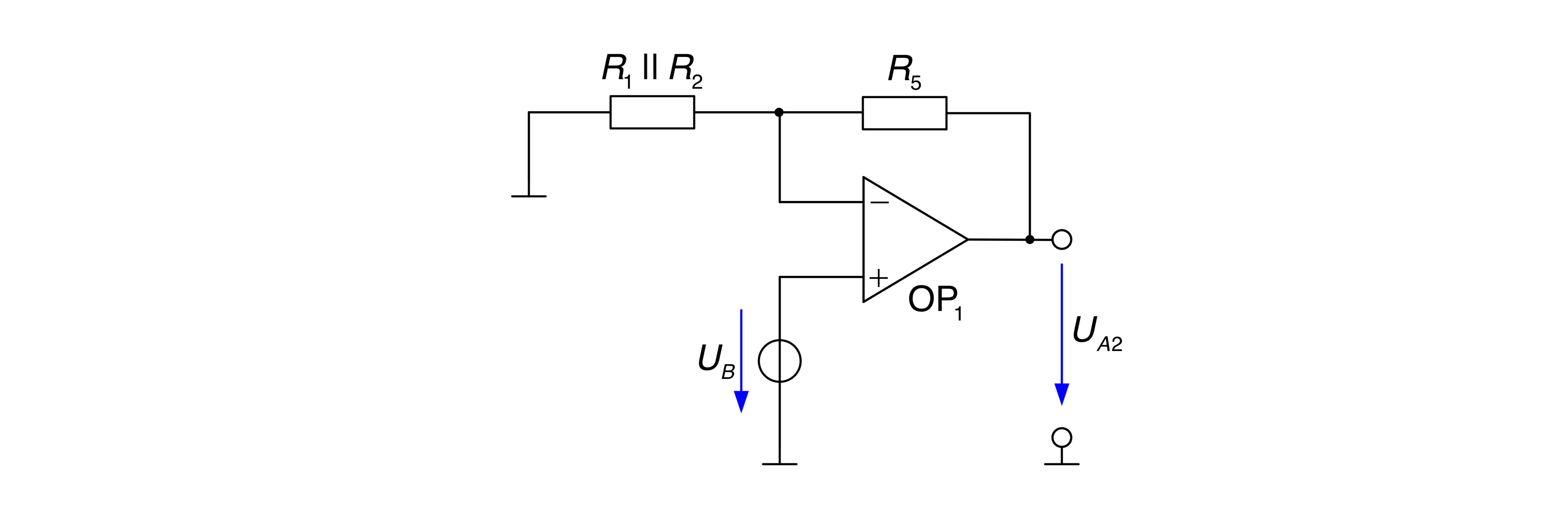
Zur Berechnung der ersten Teilspannung
Der Spannungsteiler ergibt sich zu
Ebenso kann bei der Berechnung der zweiten Teilspannung
Es gilt:
Beide Teilspannungen addiert ergeben:
Bezüglich der Spannung
Die Ausgangsspannung ist die Summe der beiden Teilspannungen.
b) Berechnen der Spannung
Das Einsetzen von Zahlenwerten ergibt
