2 / 14

by Manfred Strohrmann

(H.ErT.Z-Online)

Aufgabenstellung:

Eine Spule liegt an einer konstanten Spannungsquelle und ist mit N = 1000 Windungen Kupferdraht mehrlagig bewickelt. Der Kupferdraht hat einen Durchmesser von 0,3 mm. Die geometrischen Dimensionen der Spule können der nachfolgenden Skizze entnommen werden.

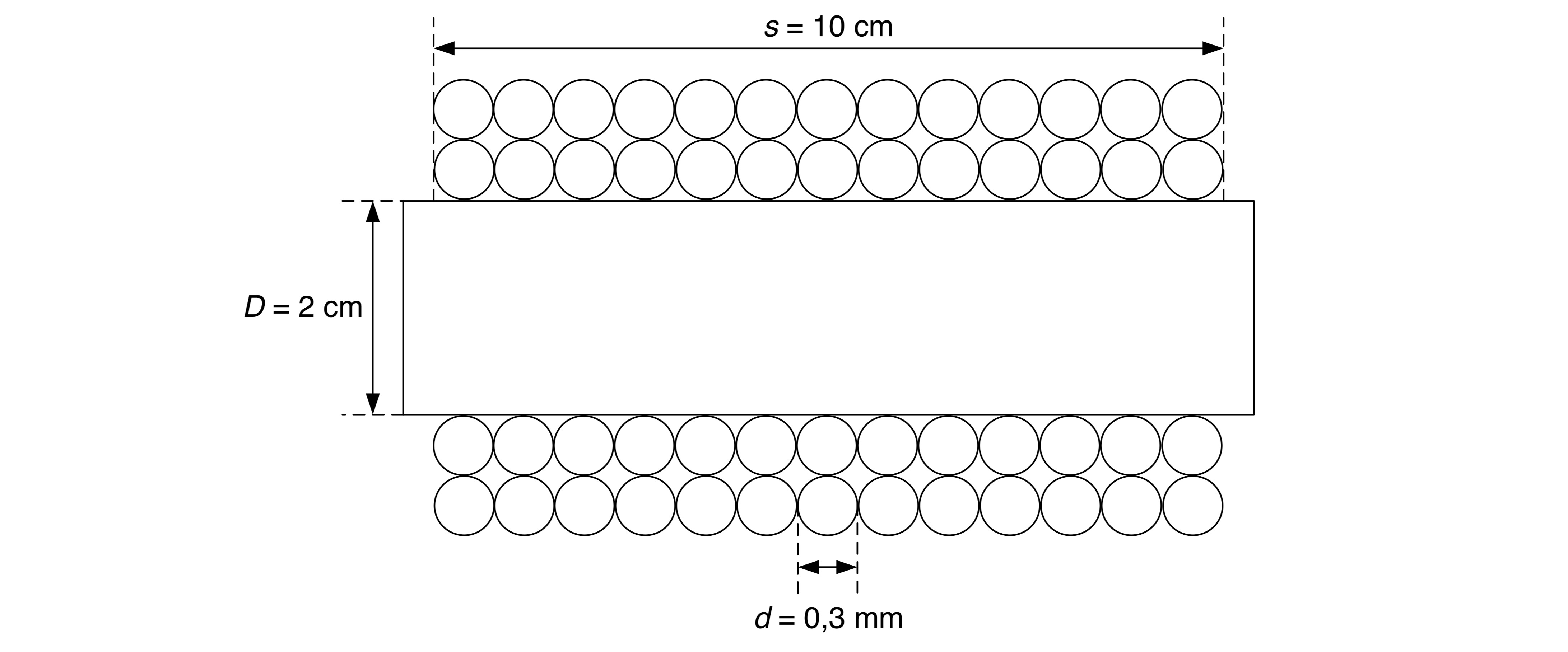
Abbildung

  1. Wie viele Lagen Kupferdraht müssen Sie auf den Spulenkörper wickeln?
  2. Wie viel Meter Kupferdraht benötigen Sie?
  3. Wie groß ist der ohmsche Widerstand der Spule bei ?

  4. Auf wie viel Prozent des ursprünglichen Stromes sinkt die Stromstärke, wenn sich die Temperatur der Wicklung von auf erhöht?

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Lagen

Berechnung der Kupferdraht Lagen:

Aus der Länge der Spule und dem Durchmesser des Spulendrahtes ergibt sich, dass n Windungen pro Lage aufgewickelt werden müssen.

Bei insgesamt 1000 Windungen muss die Spule demnach dreilagig bewickelt werden.

b) Länge

Die Durchmesser der einzelnen Wicklungslagen erstrecken sich von Drahtmitte zu Drahtmitte. Für den Umfang pro Windung in der ersten Lage gilt

Entsprechend in der zweiten und dritten Lage

Für die Gesamtlänge der Kupferlagen wird der Umfang mit der Windungszahl multipliziert.

Die Gesamtlänge aller verwendeten Lagen ergibt sich durch Addition.

c) Berechnung des Widerstands der Spule bei

Der ohmsche Widerstand der Spule bei ergibt sich über Länge und Querschnittsfläche des Drahtes zu

d) Berechnung der Stromstärke bei

Entsprechend der Temperatur weist die Spule die Widerstände und auf. Daraus ergeben sich die jeweiligen Ströme.

Steigt die Temperatur an, wird der Widerstandswert berechnet über die Gleichung

Diese Gleichung wird umgeformt

Die Widerstandsdifferenz wird durch den Ausdruck ersetzt. Bei der Temperatur vo steigt der Widerstand des Kupfer-Drahtes um

Dass der Widerstandswert steigt, ist auch zu erkennen, indem wieder eingesetzt wird.

Um den Wert, auf den die Stromstärke sinkt, zu erhalten, wird das Verhältnis zu gebildet.

Der Strom durch die Spule sinkt auf des ursprünglichen Stromes ab.

Lösung:

  1. 333,33
  4. Der Strom durch die Spule sinkt auf des ursprünglichen Stromes ab.