Aufgabenstellung:
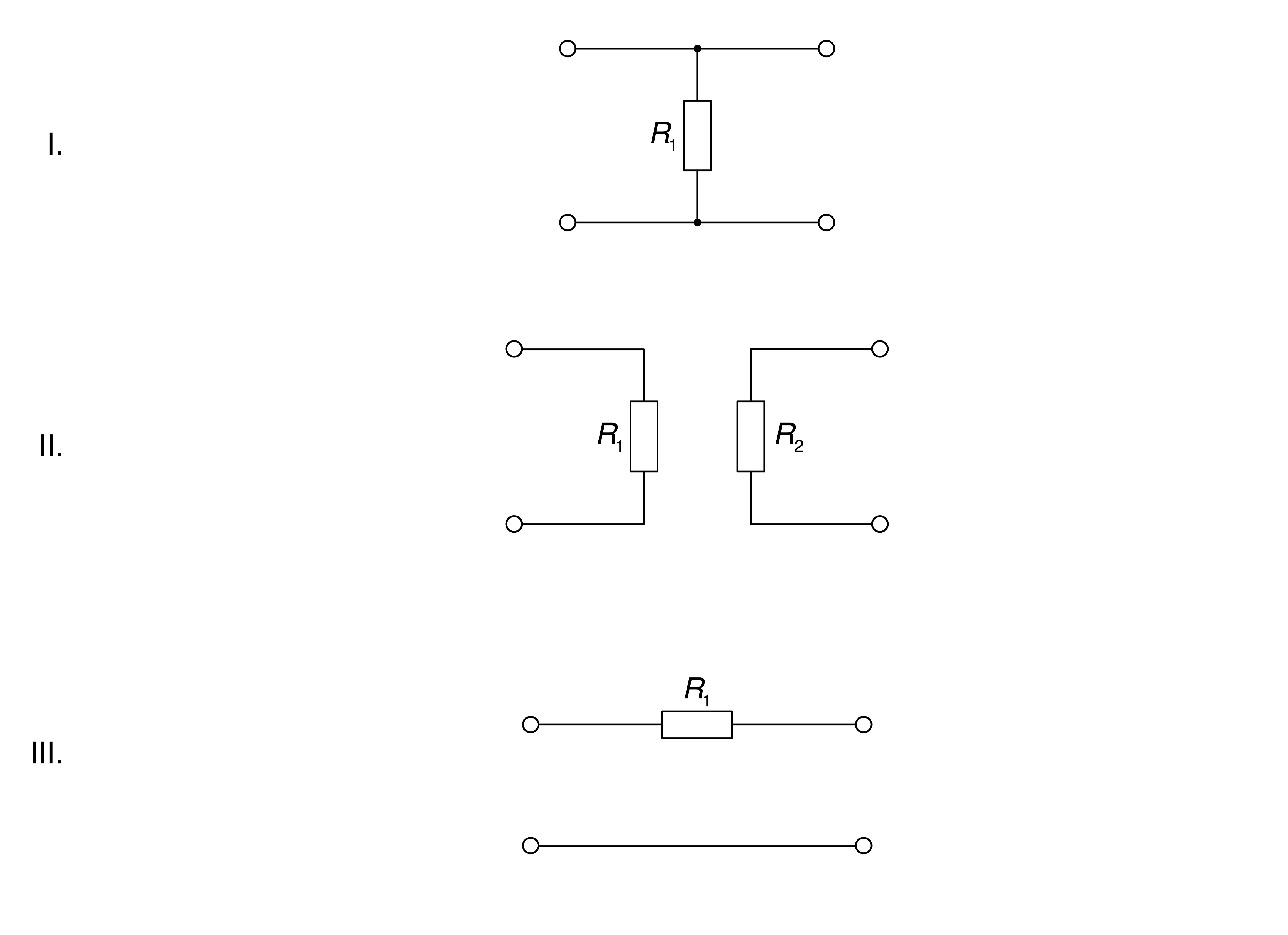
Im Folgenden sind verschiedene Vierpole abgebildet. Stellen Sie zu diesen Vierpolen die
a) Widerstand-Matrix auf und zeigen Sie dass das System kopplungssymmetrisch ist.
b) Leitwert-Matrix auf.
Lösungsweg:
a) Bestimmen der Widerstandsmatrix
Die Widerstandsmatrizen ergeben sich durch Anwendung der Gleichungen
I. Die Widerstandsmatrix für den Vierpol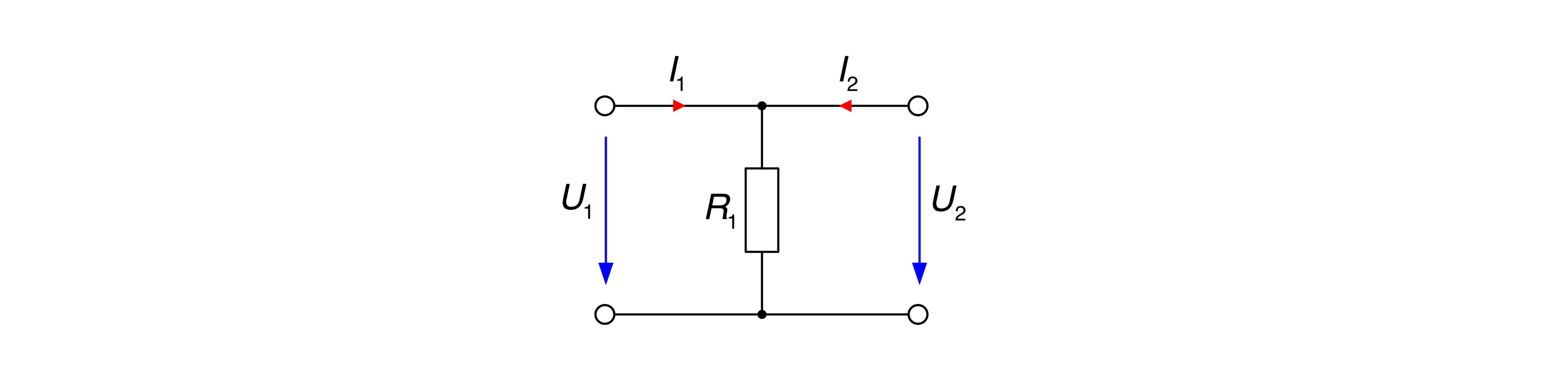
lautet
Die Matrix ist somit kopplungssymmetrisch, da gilt
II. Die Widerstandsmatrix für den Vierpol
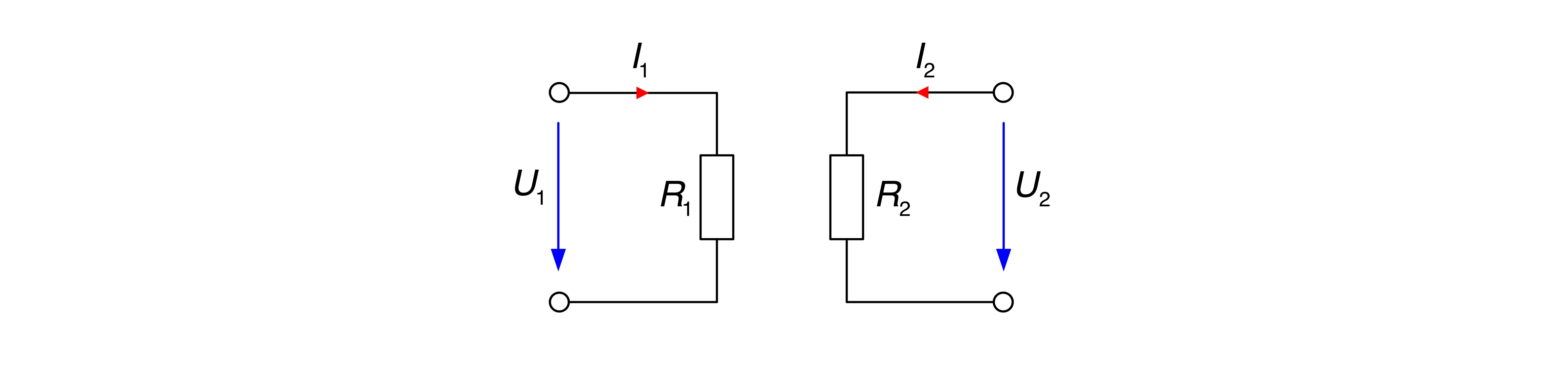
ergibt sich zu
Die Matrixelemente
III. Die Widerstandsmatrix für den Vierpol
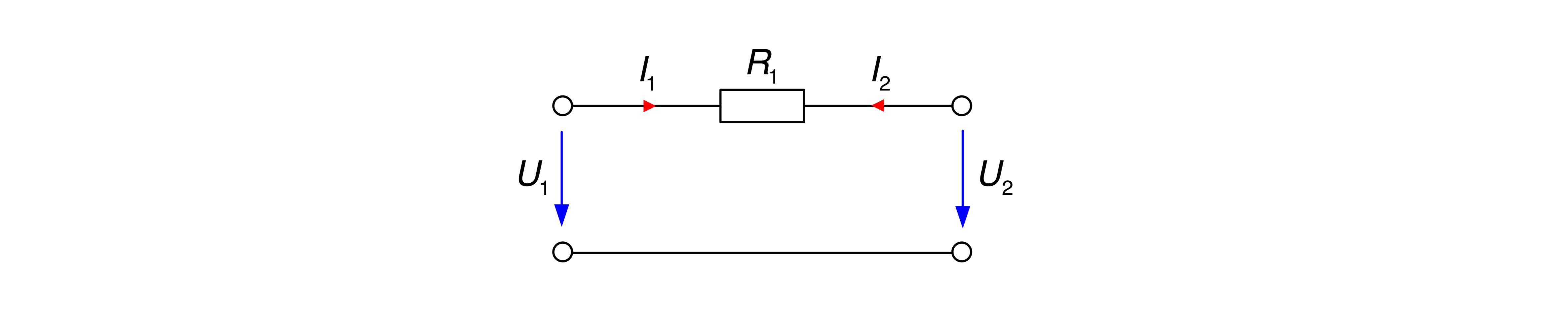
ergibt sich zu unendlich, aufgrund der Division mit
Auch im Aufgabenteil c) ist die Widerstandsmatrix kopplungssymmetrisch, denn es gilt
b) Bestimmen der Leitwertmatrix
Analog zu den Bestimmungsgleichungen für die Widerstandsmatrix ergibt sich die Leitwertmatrix aus der Anwendung der Gleichungen
I. Die Leitwertmatrix für den Vierpol
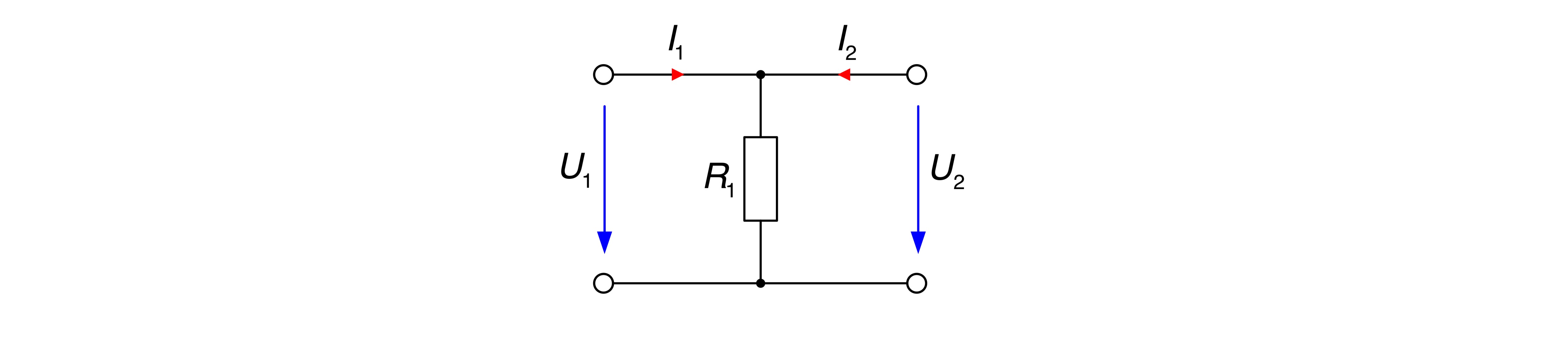
ergibt sich zu
Die Leitwerte werden aufgrund der Division mit
II. Die Leitwertmatrix für den Vierpol
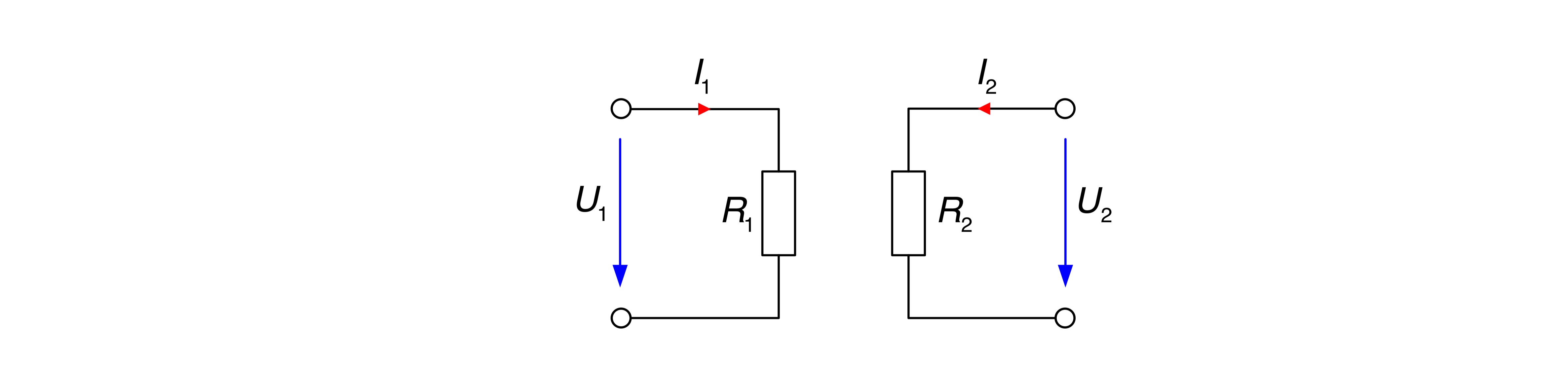
lautet
Die Matrixelemente
III. Die Leitwertmatrix für den Vierpol
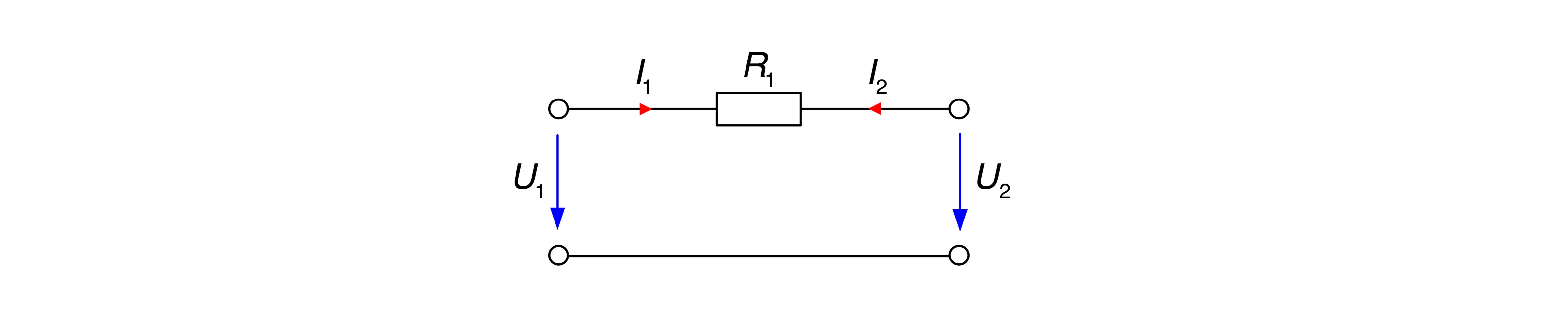
ergibt sich mit Hilfe der zu Beginn dargestellten Gleichungen zu
Der Widerstand eines Kurzschlusses ist null, der Leitwert hingegen ist unendlich. Umgekehrt ist der
Leitwert einer Unterbrechung null, allerdings der Widerstand unendlich. Aufgrund dessen gibt es Schaltungen, die lediglich mit einer Widerstandsmatrix beschrieben werden können. Andere Schaltungen lassen sich lediglich mit einer Leitwertmatrix beschreiben.
Lösung:
a)
b)
