Aufgabenstellung:
Gegeben sind zwei temperaturabhängige Widerstände
Ihre Temperaturkoeffizienten sind:
Berechnen Sie den Temperaturkoeffizienten
- Für die Reihenschaltung beider Widerstände
- Für die Parallelschaltung beider Widerstände für
- Für welchen Wert von k tritt eine Kompensation der Temperaturabhängigkeit ein?
Hinweis: Rechnen Sie bei b) mit Leitwerten und benutzen Sie die Näherung:
Lösungsweg:
Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen
a) Reihenschaltung
Speziell gilt:
b) Parallelschaltung
Parallelschaltung mit der meist berechtigten Annahme
Speziell gilt:
Setzt man wieder
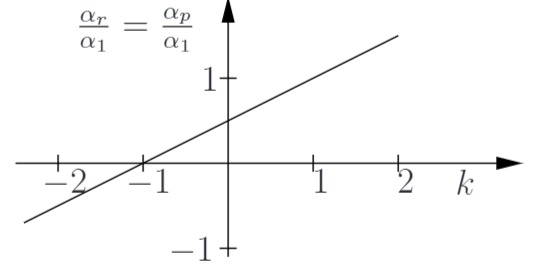
c) Kompensation der Temperaturabhängigkeiten
Die Kompensation der Temperaturabhängigkeiten tritt bei
Lösung:
a)
b)
c)