Aufgabenstellung:
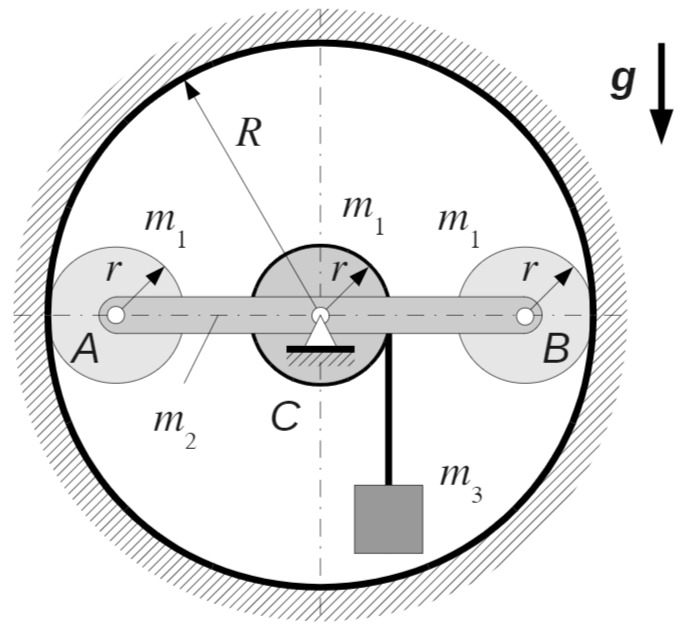 Die beiden homogenen Scheiben
Die beiden homogenen Scheiben
Die Stange
Auf der Rolle
- Ermitteln Sie die Geschwindigkeiten
und der Punkte und sowie die Winkelgeschwindigkeiten und der Scheiben und sowie der Scheibe und der Stange in Abhängigkeit von der Geschwindigkeit der Masse - Ermitteln Sie die Geschwindigkeit
der Masse in Abhängigkeit vom zurückgelegten Weg für den Fall, dass das System am Anfang in Ruhe ist. - Ermitteln Sie die Beschleunigung
der Masse .
Lösungsweg:
a) Kinematische Beziehungen
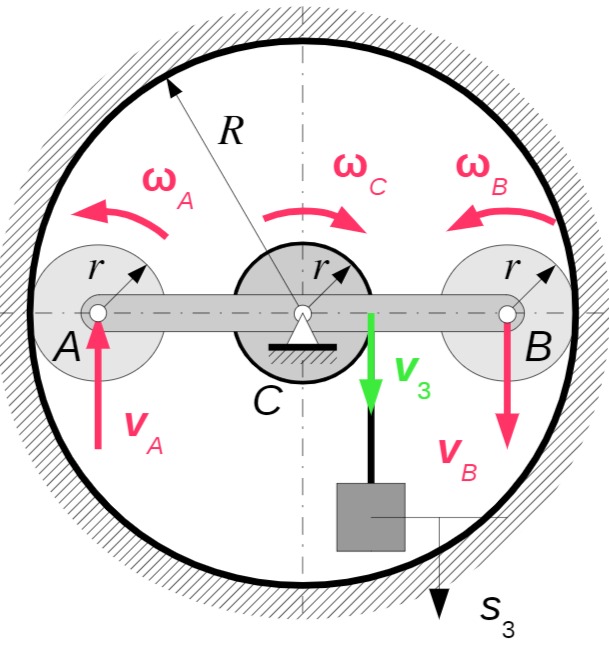 Aus
Aus
Die Punkte
Die Scheiben
b) Geschwindigkeit
Alle kinematischen Größen lassen sich in Abhängigkeit von der gesuchten Geschwindigkeit
Die einzige am System angreifende äußere Kraft ist die Gewichtskraft, die eine konservative Kraft ist. Daher kann die Aufgabe mit dem Energieerhaltungssatz gelöst werden.
Der Schwerpunkt des aus den drei Scheiben und dem Arm bestehenden Systems liegt im Punkt
Als Bezugspunkt für die Lageenergie dieses Systems wird daher Punkt
Als Bezugspunkt für die Lageenergie der Masse
Damit gilt für die Energien:
Energieerhaltungssatz:
Massenträgheitsmomente:
Mit den kinematischen Beziehungen folgt für die Geschwindigkeit
c) Beschleunigung