Aufgabenstellung:
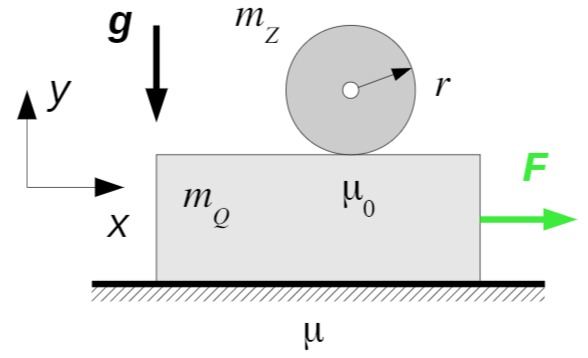 Ein homogener Zylinder (Masse
Ein homogener Zylinder (Masse
Am Quader greift die Kraft
Der Reibungskoeffizient zwischen Boden und Quader ist
Es darf angenommen werden, dass zwischen Zylinder und Quader kein Gleiten auftritt.
- Schneiden Sie die beiden Körper frei und stellen Sie alle kinetischen Gleichungen auf.
- Geben Sie die kinematische Beziehung zwischen der Geschwindigkeit
des Quaders, der Geschwindigkeit des Schwerpunkts des Zylinders und der Winkelgeschwindigkeit w des Zylinders an. Wählen Sie die Winkelgeschwindigkeit des Zylinders positiv im Gegenuhrzeigersinn. - Bestimmen Sie die Beschleunigung
des Zylinders in Abhängigkeit von der Beschleunigung des Quaders. - Bestimmen Sie die Beschleunigung
des Quaders.
Gegeben:
Lösungsweg:
Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen
a) Kinetische Gleichungen
Zylinder:
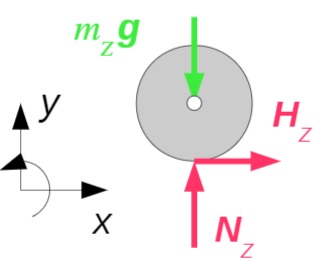
Quader:
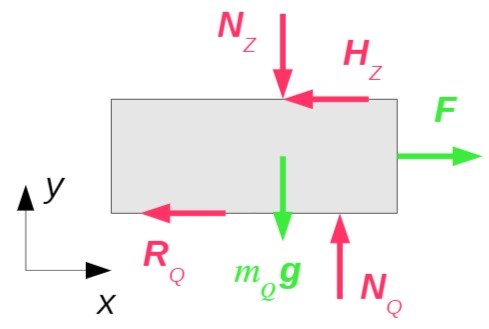
Reibungsgesetz:
b) Kinematik
Der Punkt des Zylinders, der auf dem Quader aufliegt, muss die gleiche Geschwindigkeit wie der Quader haben:
c) Beschleunigung des Zylinders
Aus (7) folgt:
Einsetzen in (3) ergibt:
Mit (1) folgt:
Auflösen nach
d) Beschleunigung des Quaders
Aus (2) folgt:
Aus(5) folgt:
Einsetzen in (6) ergibt:
Einsetzen in (4) ergibt:
Auflösen nach
Lösung:
- Siehe Lösungsweg.