Rotation um eine feste Achse

Allgemeine ebene Bewegung

Systeme von starren Körpern

Ungleichungen 

Statik in der Ebene

Fourier-Reihen

Funktionsfolgen

Unterschied In/Homogen

Basis, Basiswechsel

Abbildungsmatrizen

Funktionen bestimmen

Geraden und Ebenen

Gruppen

lineare abbildung 

quadratische ergänzung

Baustatik 1

Anfangswertprobleme :)

Differentialgleichungen

basis 

QR-Algorithmus

QR-Zerlegung

Cholesky-Zerlegung

Bild & Urbild

Zweigstromanalyse

Transistor als Thermometer

Investment

Teilfolgen

Epsilon Delta Kriterium

prinzip der virtuellen verrückung 

Linear Kombination

Folgen, Reihen und Potenzreihen

Flächenpressung

Arbeit 

Cholesky Zerlegung

Polynomfunktionen beschreiben

Zu Maß-und Integrationstheorie: Majorisierte Konvergenz

Teilchenphysik und Festkörperphysik

Orthogonaltrajektorien

test

Taylorreihen

Regel von de L'Hopital

Mathe

KRAFT

Grenzwert Funktion 

Folgenkriterium

ϵ-δ Kriterium 

Beweis Stetigkeit 

Wahrheitstabelle

2x2 Matrix

Matrix invertieren

Basiswechselsatz

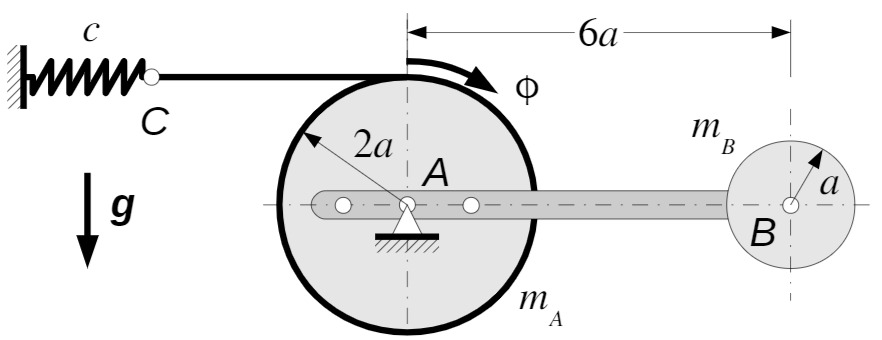Lineare Abbildunge 

Vorderrad fahradgabel lagerkräfte berechnen 

Spannungsregelung

Jordan Normal Form

Test

Induktion 

Jordan-Normalform

Ansatz der Störfunktion zur Bestimmung der Partikulären Lösung

Kurvenintegral

dlg mithilfe inhomogenen linearen system lösen

Inverse einer Matrix

Gleichmäßige Stetigkeit

addition

Regel von L´Hospital

Lineare Abbildungen

dimension eines Untervektorraumes bestimmen

Stationäre Stoffübertragung

Polplan, Prinzip der virtuellen Verrückungen

komplexe Ungleichungen 

Bidualräume

Dualräume

Taylorpolynome

Kern und Basis

Diagonalisieren einer Matrix

Rekursive Folgen

Exponentialreihe

Darstellungsmatrizen

restglied

Basiswechsel

Gamma Funktion

Newton Verfahren

Randwertaufgabe

Numerische Integration: Trapez- und Simpsonregel

Funktionenfolgen

dualräume

Dualraum

Komplexe Nullstellen

Chemie

Natascha Kirchmann

Differentialquotient

Folgedefinition des Funktionslimes

Grenzwerte und Stetigkeit 

Komplexe Zahlen

Kern und Bild 

Direkte Summe 

<ol style="list-style-type: lower-alpha;">
<li>\[J^{A}=200 m a^{2}\]</li>
<li>\[\omega=\sqrt{\frac{3}{10} \frac{g}{a} \sin (\phi)-\frac{1}{50} \frac{c}{m} \phi^{2}}\]</li>
<li>\[\dot{\omega}=\frac{3}{20} \frac{g}{a} \cos (\phi)-\frac{1}{50} \frac{c}{m} \phi\]</li>
</ol>

<p>Einsetzen und Zusammenfassen ergibt:</p>


<p>\[<br />J^{A}=\left(2 \cdot 9+\frac{2}{5} \cdot 5+5 \cdot 36\right) m a^{2}=200 m a^{2}<br />\]</p>


<p>Zustand \( A: \) dargestellte Lage;</p>
<p>Zustand \( B \) : beliebige ausgelenkte Lage</p>
<p>Nullniveau für die Lageenergie der Kugel: Lage im Zustand \( A \)</p>


<p>Zustand <mjx-container class="MathJax" jax="SVG"><svg alt=" A: " style="vertical-align: 0" xmlns="http://www.w3.org/2000/svg" width="2.954ex" height="1.62ex" role="img" focusable="false" viewBox="0 -716 1305.8 716" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2690-TEX-I-1D434" d="M208 74Q208 50 254 46Q272 46 272 35Q272 34 270 22Q267 8 264 4T251 0Q249 0 239 0T205 1T141 2Q70 2 50 0H42Q35 7 35 11Q37 38 48 46H62Q132 49 164 96Q170 102 345 401T523 704Q530 716 547 716H555H572Q578 707 578 706L606 383Q634 60 636 57Q641 46 701 46Q726 46 726 36Q726 34 723 22Q720 7 718 4T704 0Q701 0 690 0T651 1T578 2Q484 2 455 0H443Q437 6 437 9T439 27Q443 40 445 43L449 46H469Q523 49 533 63L521 213H283L249 155Q208 86 208 74ZM516 260Q516 271 504 416T490 562L463 519Q447 492 400 412L310 260L413 259Q516 259 516 260Z"></path><path id="MJX-2690-TEX-N-3A" d="M78 370Q78 394 95 412T138 430Q162 430 180 414T199 371Q199 346 182 328T139 310T96 327T78 370ZM78 60Q78 84 95 102T138 120Q162 120 180 104T199 61Q199 36 182 18T139 0T96 17T78 60Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mi"><use data-c="1D434" xlink:href="#MJX-2690-TEX-I-1D434"></use></g><g data-mml-node="mo" transform="translate(1027.8,0)"><use data-c="3A" xlink:href="#MJX-2690-TEX-N-3A"></use></g></g></g></svg></mjx-container> dargestellte Lage;</p>
<p>Zustand <mjx-container class="MathJax" jax="SVG"><svg alt=" B " style="vertical-align: 0" xmlns="http://www.w3.org/2000/svg" width="1.717ex" height="1.545ex" role="img" focusable="false" viewBox="0 -683 759 683" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2691-TEX-I-1D435" d="M231 637Q204 637 199 638T194 649Q194 676 205 682Q206 683 335 683Q594 683 608 681Q671 671 713 636T756 544Q756 480 698 429T565 360L555 357Q619 348 660 311T702 219Q702 146 630 78T453 1Q446 0 242 0Q42 0 39 2Q35 5 35 10Q35 17 37 24Q42 43 47 45Q51 46 62 46H68Q95 46 128 49Q142 52 147 61Q150 65 219 339T288 628Q288 635 231 637ZM649 544Q649 574 634 600T585 634Q578 636 493 637Q473 637 451 637T416 636H403Q388 635 384 626Q382 622 352 506Q352 503 351 500L320 374H401Q482 374 494 376Q554 386 601 434T649 544ZM595 229Q595 273 572 302T512 336Q506 337 429 337Q311 337 310 336Q310 334 293 263T258 122L240 52Q240 48 252 48T333 46Q422 46 429 47Q491 54 543 105T595 229Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mi"><use data-c="1D435" xlink:href="#MJX-2691-TEX-I-1D435"></use></g></g></g></svg></mjx-container> : beliebige ausgelenkte Lage</p>
<p>Nullniveau für die Lageenergie der Kugel: Lage im Zustand <mjx-container class="MathJax" jax="SVG"><svg alt=" A " style="vertical-align: 0" xmlns="http://www.w3.org/2000/svg" width="1.697ex" height="1.62ex" role="img" focusable="false" viewBox="0 -716 750 716" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2692-TEX-I-1D434" d="M208 74Q208 50 254 46Q272 46 272 35Q272 34 270 22Q267 8 264 4T251 0Q249 0 239 0T205 1T141 2Q70 2 50 0H42Q35 7 35 11Q37 38 48 46H62Q132 49 164 96Q170 102 345 401T523 704Q530 716 547 716H555H572Q578 707 578 706L606 383Q634 60 636 57Q641 46 701 46Q726 46 726 36Q726 34 723 22Q720 7 718 4T704 0Q701 0 690 0T651 1T578 2Q484 2 455 0H443Q437 6 437 9T439 27Q443 40 445 43L449 46H469Q523 49 533 63L521 213H283L249 155Q208 86 208 74ZM516 260Q516 271 504 416T490 562L463 519Q447 492 400 412L310 260L413 259Q516 259 516 260Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mi"><use data-c="1D434" xlink:href="#MJX-2692-TEX-I-1D434"></use></g></g></g></svg></mjx-container></p>


<p>\[<br />\begin{array}{|c|c|c|}<br />\hline &amp; \text { Zustand } A &amp; \text { Zustand } B \\<br />\hline E^{G} &amp; 0 &amp; -6 a \sin (\phi) m_{B} g \\<br />\hline E^{F} &amp; 0 &amp; \frac{1}{2} c(2 a \phi)^{2} \\<br />\hline E^{K} &amp; 0 &amp; \frac{1}{2} J^{A} \omega^{2} \\<br />\hline<br />\end{array}<br />\]</p>


<p>\[<br />0=-6 a \sin (\phi) m_{B} g+2 c a^{2} \phi^{2}+\frac{1}{2} J^{A} \omega^{2}<br />\]</p>


<p>\[<br />100 m a^{2} \omega^{2}=30 m g a \sin (\phi)-2 c a^{2} \phi^{2}<br />\]</p>


<p>\[<br />\begin{align}<br />\omega^{2}&amp;=\frac{3}{10} \frac{g}{a} \sin (\phi)-\frac{1}{50} \frac{c}{m} \phi^{2} \\\\<br />\omega&amp;=\sqrt{\frac{3}{10} \frac{g}{a} \sin (\phi)-\frac{1}{50} \frac{c}{m} \phi^{2}}<br />\end{align}<br />\]</p>


<p>\[<br />\dot{\omega}=\frac{1}{2} \frac{d \omega^{2}}{d \phi}=\frac{3}{20} \frac{g}{a} \cos (\phi)-\frac{1}{50} \frac{c}{m} \phi<br />\]</p>

<p><img style="float: right;" src="https://storage.googleapis.com/max-academy-image-bucket/6048f152c08c49af0713d509.png" alt="Abbildung" width="66%" />Der abgebildete starre Körper besteht aus einer homogenen Scheibe (Radius \( 2 a, \) Masse \( m_{A} \) und einer homogenen Kugel (Radius \( a, \) Masse \( \left.m_{B}\right), \) die durch eine masselose Stange starr miteinander verbunden sind. Er ist im Punkt \( A \) reibungsfrei gelenkig gelagert.<br />Auf der Scheibe ist ein masseloses dehnstarres Seil aufgespult, das im Punkt \( C \) an eine lineare Feder mit der Federkonstanten \( c \) angeschlossen ist.</p>
<p>In der dargestellten Lage ist die Feder entspannt, und der starre Körper ist in Ruhe.</p>
<ol style="list-style-type: lower-alpha;">
<li>Bestimmen Sie das Massenträgheitsmoment \( J^{A} \) des starren Körpers bezüglich des Punktes \( A \).</li>
<li>Bestimmen Sie mithilfe des Energieerhaltungssatzes die Winkelgeschwindigkeit \( \omega=\dot{\phi} \) in Abhängigkeit vom Winkel \( \phi . \)</li>
<li>Bestimmen Sie die Winkelbeschleunigung \( \dot{\omega} \) in Abhängigkeit vom Winkel \( \phi.\)</li>
</ol>
<p><strong>Gegeben: </strong>\( a, \ c, \ m, \ m_{A}=9 m, \ m_{B}=5 m \)</p>

Dies ist eine interaktive Aufgabe zu: Rotation um eine feste Achse mit praktischen Tipps zum Lösen und einer Zusammenfassung der nötigen Theorie

Kinetik des starren Körpers - Rotation um eine feste Achse | Aufgabe m

Aufgabenstellung:

Lösungsweg:

Lösung: