Aufgabenstellung:
Eine homogene Kugel (Masse
beschrieben wird. Dabei wird die Ortskoordinate
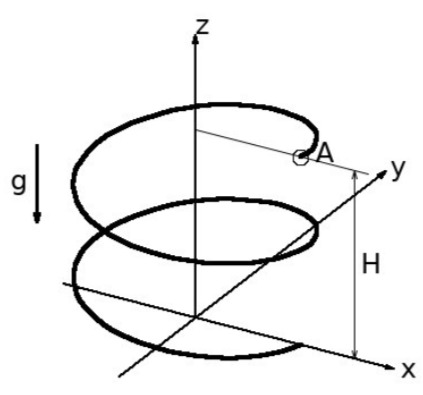 Bestimmen Sie die Bahngeschwindigkeit
Bestimmen Sie die Bahngeschwindigkeit und die Bahnbeschleunigung . Verwenden Sie dazu den Energieerhaltungssatz. - Bestimmen Sie das Geschwindigkeits-Zeit-Gesetz
und das OrtZeit-Gesetz wenn die Kugel sich zum Zeitpunkt im Punkt befindet. - Berechnen Sie den Einheitstangentenvektor
. - Berechnen Sie die Normalbeschleunigung
Gegeben:
Lösungsweg:
a) Bahngeschwindigkeit und Bahnbeschleunigung
Wenn das Nullniveau für die Lageenergie in die
Damit lautet der Energieerhaltungssatz:
Massenträgheitsmoment, Rollbedingung und Ausdruck für
Einsetzen in den Energieerhaltungssatz und nach
Für die Bahnbeschleunigung folgt:
b) Geschwindigkeit-Zeit-Gesetz und Ort-Zeit-Gesetz
Die Bahnbeschleunigung ist konstant. Damit handelt es sich um eine gleichmäßig beschleunigte Bewegung.
Geschwindigkeit-Zeit-Gesetz:
Ort-Zeit-Gesetz:
c) Einheitstangentenvektor
d) Normalbeschleunigung
Für den Vektor der Normalbeschleunigung gilt:
Mit
folgt für den Betrag der Normalbeschleunigung: