Aufgabenstellung:
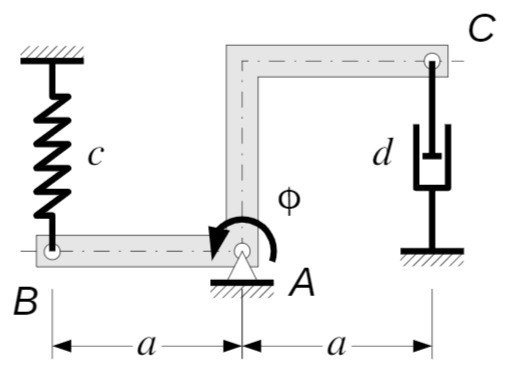 Der starre Rahmen
Der starre Rahmen
- Stellen Sie die Schwingungsgleichung auf und ermitteln Sie die Eigenkreisfrequenz
der freien ungedämpften Schwingung und die Abklingkonstante in Abhängigkeit von und . - Eine Messung der Vertikalbeschleunigung im Punkt
zeigt, dass zwei benachbarte Maxima einen zeitlichen Abstand von haben und das Verhältnis zwischen zwei aufeinanderfolgenden Maxima beträgt. Ermitteln Sie daraus die Werte der Dämpfungskonstanten , der Eigenkreisfrequenz und des Lehrschen Dämpfungsmaßes
Der Winkel
Lösungsweg:
a) Schwingungsgleichung
Drallsatz bezüglich
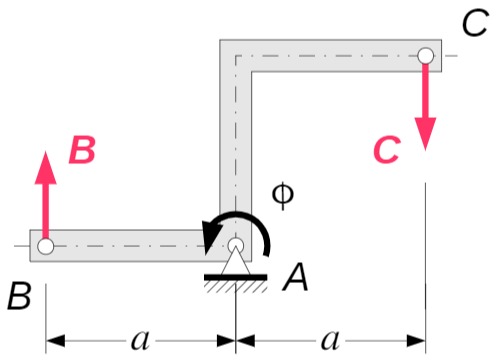
Federkraft:
Dämpferkraft:
Einsetzen in den Drallsatz ergibt:
Aus der Schwingungsgleichung kann abgelesen werden:
b) Abklingkonstante, Kreisfrequenz und Lehrsches Dämpfungsmaß
Periode der gedämpften Schwingung:
Aus
Für die Kreisfrequenz der gedämpften Schwingung gilt:
Aus
Damit berechnet sich die Eigenkreisfrequenz der ungedämpften Schwingung zu
Das Lehrsche Dämpfungsmaß berechnet sich zu