4 / 11

Aufgabenstellung:

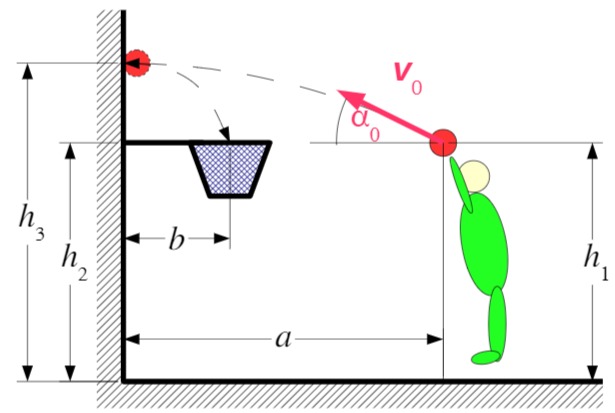
Abbildung

Ein Basketballspieler hat den Abstand zur Wand, an der der Korb hängt. Er möchte den Ball so werfen, dass er in der Höhe senkrecht auf die Wand trifft und anschließend in der Mitte des Korbs landet. Die Mitte des Korbs befindet sich in der Höhe und hat den Abstand von der Wand.

  1. Mit welcher Geschwindigkeit muss der Ball auf die Wand auftreffen?
  2. Aus welcher Höhe muss der Ball geworfen werden, und wie groß müssen Wurfgeschwindigkeit und Wurfwinkel sein?

Gegeben:
Stoßzahl:

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Auftreffgeschwindigkeit

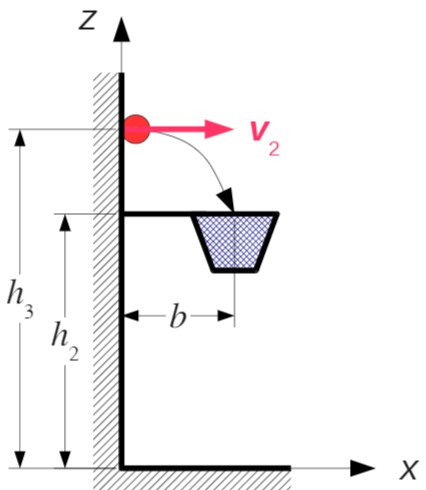AbbildungDer Ball trifft mit der Geschwindigkeit auf die Wand und hat nach dem Stoß die Geschwindigkeit Die Geschwindigkeit wird aus der Bedingung berechnet, dass der Ball in der Mitte des Korbes landet.

Der Wurfwinkel für den auf den Stoß folgenden Wurf ist

Damit lautet die Gleichung der Flugbahn im eingezeichneten Koordinatensystem:

Die Geschwindigkeit lässt sich aus der Bedingung berechnen:

Daraus folgt:

Aus folgt für die Geschwindigkeit :

Zahlenwerte:

b) Wurfhöhe, Wurfgeschwindigkeit und Wurfwinkel

Der schiefe Wurf wird im eingezeichneten Koordinatensystem betrachtet. Die Wurfhöhe wird an der Wand erreicht, die sich an der Stelle befindet.

Die Gleichung für die Wurfbahn lautet:

Da die Geschwindigkeit in -Richtung konstant ist, gilt für

Einsetzen in die Gleichung für die Wurfbahn führt auf

Da der Ball senkrecht auf die Wand trifft, gilt:

Damit berechnet sich die Höhe zu

Für die gesuchte Höhe gilt:

Für die Wurfgeschwindigkeit folgt:

Zahlenwerte:

Lösung: