4 / 4

Aufgabenstellung:

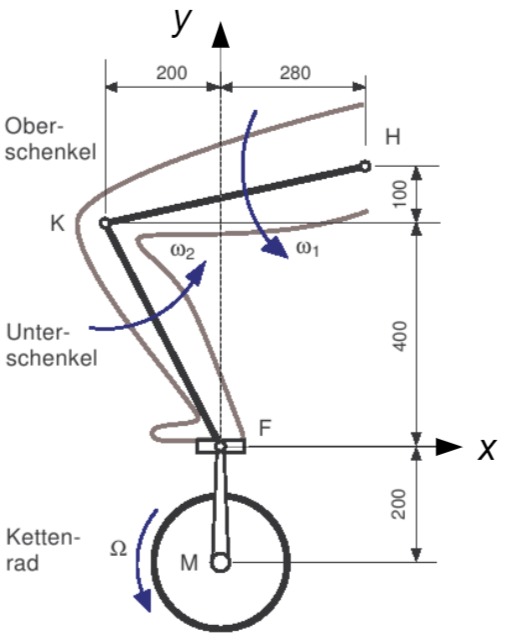
Abbildung

Beim Fahrradfahren wird die Bewegung der Beine über das Pedal auf die Drehung des Kettenrades übertragen.
Das Bein wird über einen zweigliedrigen Gelenkmechanismus modelliert, der im Hüftgelenk mit dem Fahrrad und im Fußgelenk mit dem Pedal verbunden ist.

  1. Bestimmen Sie für die dargestellte Stellung die Koordinaten des Momentanpols des Unterschenkels im angegebenen Koordinatensystem.
  2. Mit welchen Winkelgeschwindigkeiten und müssen in der dargestellten Stellung Ober- und Unterschenkel bewegt werden, damit sich das Kettenrad mit der Winkelgeschwindigkeit dreht?

Gegeben:

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Momentanpol des Unterschenkels

Skizze:

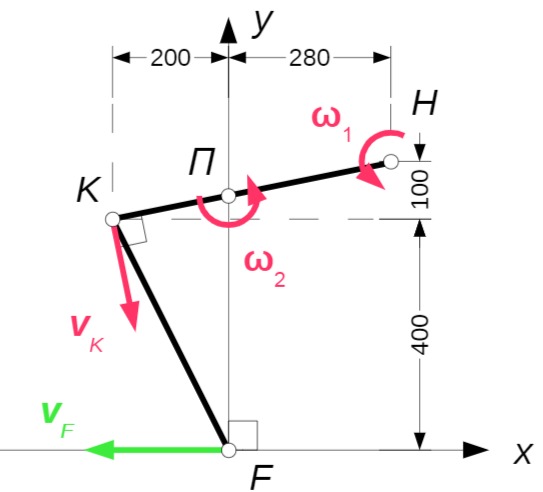AbbildungDie Geschwindigkeit von Punkt zeigt in Richtung der negativen -Achse.

Punkt bewegt sich auf einer Kreisbahn um Punkt . Seine Geschwindigkeit steht daher senkrecht auf der Geraden

Der Momentanpol ist der Schnittpunkt der -Achse, die senkrecht auf steht, und der Geraden , die senkrecht auf steht.

Die -Koordinate des Momentanpols berechnet sich aus

b) Winkelgeschwindigkeiten

In der gezeichneten Lage dreht sich der Unterschenkel mit der Winkelgeschwindigkeit um den Momentanpol . Für die Geschwindigkeit von Punkt gilt daher:

Der Punkt dreht sich aber auch mit der Winkelgeschwindigkeit um den Mittelpunkt des Kettenrads. Daher gilt auch:

Aus diesen beiden Gleichungen folgt für die Winkelgeschwindigkeit des Unterschenkels:

Als Teil des Unterschenkels dreht sich das Knie mit der Winkelgeschwindigkeit um den Momentanpol des Unterschenkels. Daher gilt für seine Geschwindigkeit:

Als Teil des Oberschenkels dreht sich das Knie mit der Winkelgeschwindigkeit um Punkt . Daher gilt für seine Geschwindigkeit auch:

Aus diesen beiden Gleichungen berechnet sich die Winkelgeschwindigkeit des Oberschenkels zu

Aus Ähnlichkeitsbetrachtungen folgt für :

Zahlenwert:

Lösung: