Aufgabenstellung:
Ein Kondensator mit der Kapazität
Es ist der zeitliche Verlauf der Kondensatorspannung
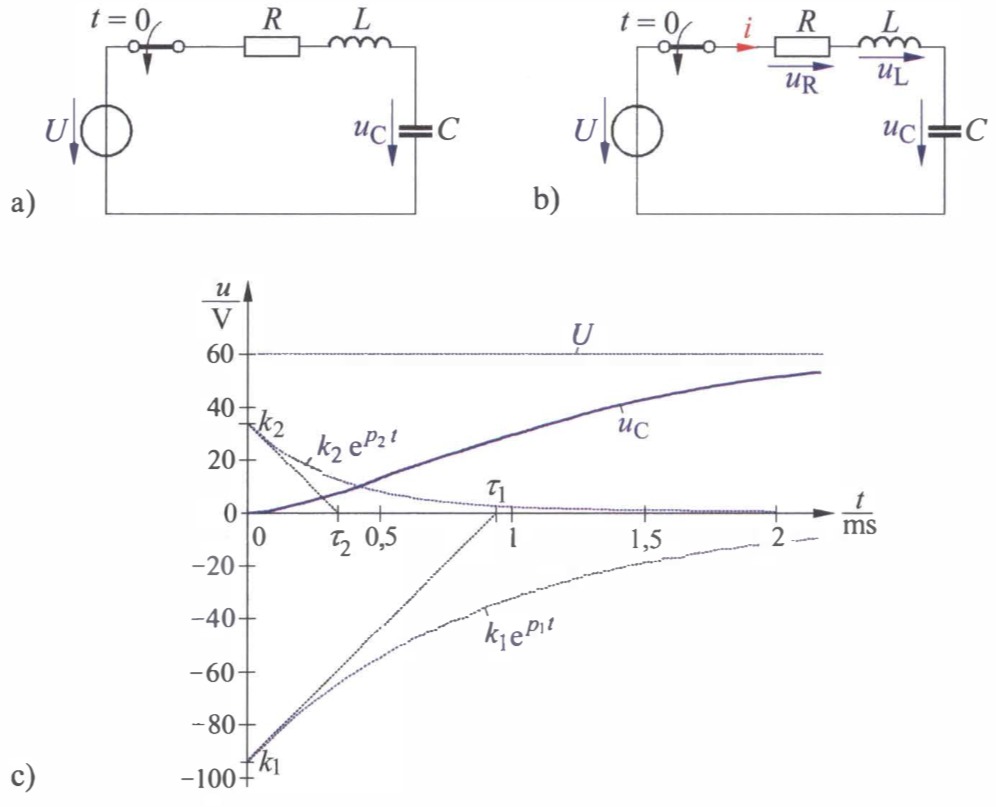
Bild: Aufladen eines Kondensators über eine RL-Reihenschaltung. a) Gegebene Schaltung,
b) Schaltung mit eingetragenen Teilspannungen und eingetragenem Strom, c) zeitlicher Verlauf der Kondensatorspannung
Lösungsweg:
Wir führen nach Bild b die Teilspannungen
Mit
Wir erhalten also eine inhomogene Differenzialgleichung 2. Ordnung. Zu deren Lösung verwenden wir den Ansatz
Hierin stellt
Durch Subtraktion ergibt sich:
Hieraus folgt, wenn wir alle Ausdrücke durch
Die Bestimmung der stationären Kondensatorspannung
einstellt.
Zur Ermittlung der freien Kondensatorspannung
Darin sind
Setzen wir ein, so ergibt sich
Wir teilen alle Ausdrücke durch
Ihre beiden Lösungen lauten
Damit ergibt sich für die freie Kondensatorspannung die allgemeine Lösung
Zur Bestimmung der hierin enthaltenen Konstanten
Somit lautet die allgemeine Lösung für die Kondensatorspannung:
Da die für
Weiterhin muss im Zeitpunkt
Setzen wir hierin die Anfangsbedingung
Hieraus folgt mit
Damit stellen diese zwei Gleichungen mit zwei Unbekannten dar. Setzen wir die Zahlenwerte ein, so erhalten wir (in Matrizenschreibweise)
Die Lösungen sind
Damit lautet die endgültige Lösung für den Verlauf der Kondensatorspannung
Die Kondensatorspannung steigt also nach der angegebenen Gleichung vom Anfangswert