Aufgabenstellung:
In der Schaltung nach Bild a wird die Reihenschaltung eines Kondensators mit der Kapazität
Es ist der zeitliche Verlauf der Kondensatorspannung
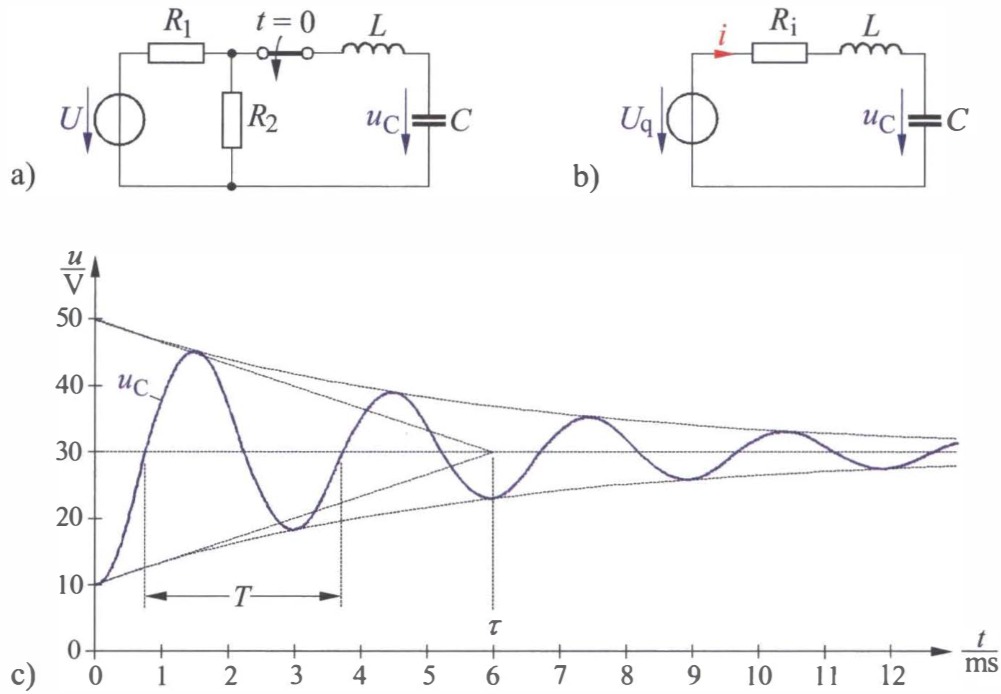
Bild : Schaltvorgang in einem RLC-Stromkreis. a) Gegebene Schaltung, b) elektrisch gleichwertige Ersatzschaltung, c) zeitlicher Verlauf der Kondensatorspannung
Lösungsweg:
Wir ersetzen zunächst den in Bild a aus der Spannungsquelle sowie den Widerständen
und der Innenwiderstand
Es lautet die Differenzialgleichung zur Bestimmung von
Zu deren Lösung wählen wir den Ansatz
Hierbei ist aus Bild b ersichtlich, dass die stationäre Kondensatorspannung
beträgt. Für die freie Kondensatorspannung
Für die hierin enthaltenen Konstanten
Wir erhalten also für
darstellen, wobei im vorliegenden Fall
Dabei sind
Die hierin enthaltenen Konstanten
Weiterhin muss im Zeitpunkt
Setzen wir hierin die Bedingung
Hieraus folgt mit
Damit erhalten wir
Setzen wir die gefundenen Werte ein, so finden wir die endgültige Lösung für den Verlauf der Kondensatorspannung als
Die Kondensatorspannung erreicht also - mit einer gedämpften Schwingung der Kreisfrequenz
und die Zeitkonstante des Abklingvorgangs
In Bild c ist der zeitliche Verlauf der Kondensatorspannung