Aufgabenstellung:
Die Schaltung nach Bild (a) enthält den ohmschen Widerstand
Welche Werte haben der ohmsche Widerstand
Lösungsweg:
Bestimmen von
Wir bestimmen zunächst den von der Spannungsquelle gelieferten (und im Widerstand
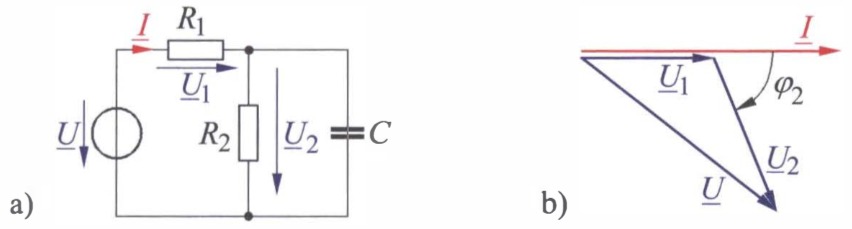
Danach zeichnen wir zu der in Bild a angegebenen Schaltung das in Bild b dargestellte Zeigerdiagramm. Wir berücksichtigen dabei, dass die Spannung
Aus der Gleichung
finden wir den Betrag des Winkels
Damit beträgt der gesuchte Winkel (in Bild b)
Mit diesem Ergebnis können wir den Strom
Damit gilt in Bild a für die aus
Wir setzen die Real- und die Imaginärteile jeweils für sich gleich und erhalten die Ergebnisse