Aufgabenstellung:

Das Oszillogramm (Abbildung b) zeigt die beiden Wechselströme
a) die Scheitelwerte
b) den Scheitelwert
I. mit Berücksichtigung der Nullphasenwinkel
II. ohne Berücksichtigung der Nullphasenwinkel
und rechnerisch.
Lösungsweg:
Allgemein
Zunächst muss hier der Typ der harmonischen Zeitfunktion geklärt werden.
Wie üblich nehmen wir daher an, es handelt sich um eine Kosinunsfunktion.
a) Scheitelwerte und Nullphasenwinkel
Man ließt in dem Graphen den Scheitelwert der Kosinusfunktion ab und zieht diesen Punkt dann auf
Aus dem Diagramm liest man für
Periodendauer
Der Scheitelpunkt liegt etwa bei
Da der positive Scheitelwert rechst der Bildanfangs liegt:
Die Funktion sieht daher so aus:
Für
Periodendauer
Der Scheitelpunkt liegt etwa bei
Da der positive Scheitelwert rechst der Bildanfangs liegt:
Die Funktion sieht daher so aus:
Die Phasenverschiebung zwischen den Strömen ist gleich der Differenz zwischen den Nullphasenwinkeln
Also eilt der Strom
Dies entspricht
b) Scheitelwert und Phasenlage
Lösung mit Zeigerdiagrammen unter Berücksichtigung der Nullphasenwinkel
Das Vorgehen sieht dabei wie folgt aus:
a)
b)
c)
d) der Winkel
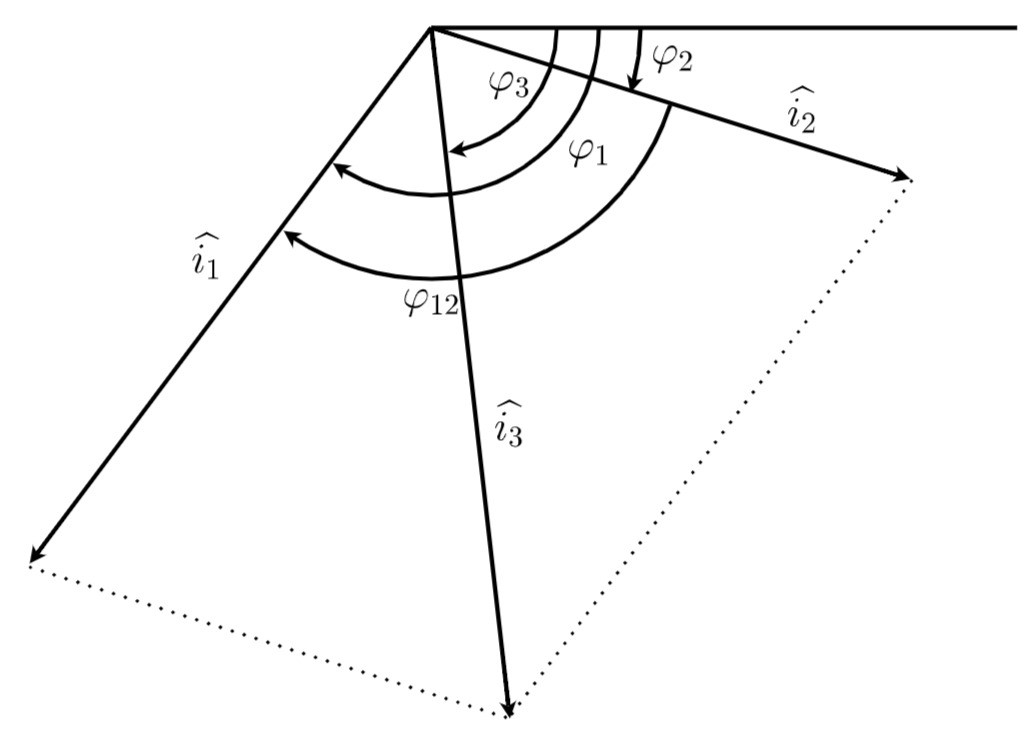
Graphische Lösung unter Berückichtiguung des Nullphasenwinkels
Lösung mit Zeigerdiagrammen ohne Berücksichtigung der Nullphasenwinkel
Das Vorgehen sieht dabei wie folgt aus:
a)
b)
c)
d) der Winkel
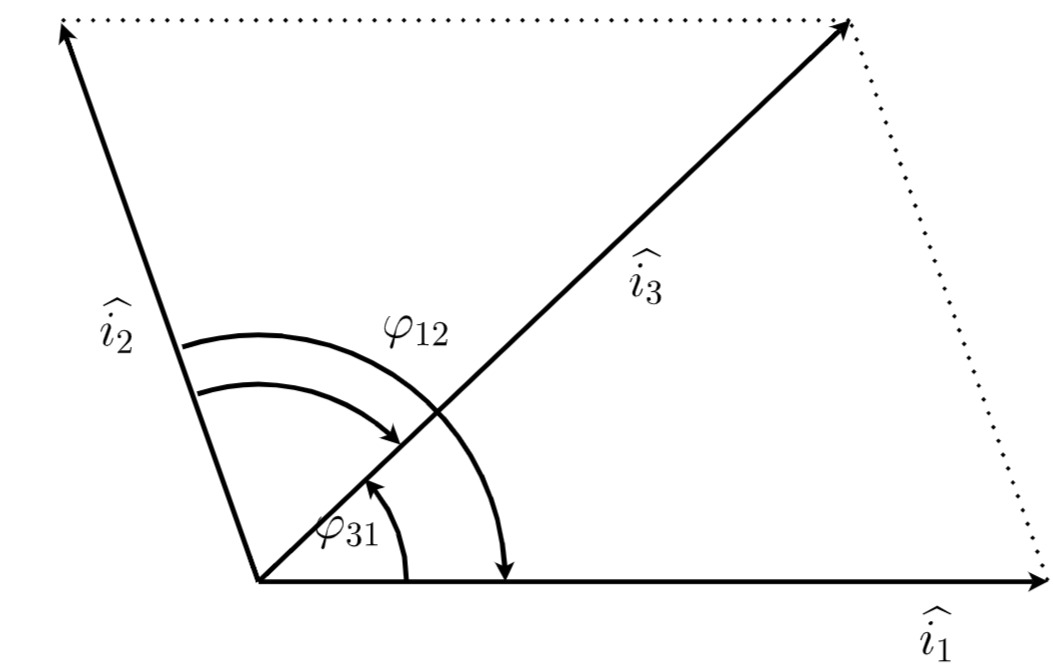
Graphische Lösung ohne Berückichtiguung des Nullphasenwinkels
Analytische Lösung unter Berücksichtigung der Nullphasenwinkel
Der Gesamtstrom lässt sich berechnen mit der Formel
Der Winkel berechnet sich nach der Formel
Der Winkel zwischen dem resultierenden Strom und dem Strom
Analytische Lösung ohne Berücksichtigung der Nullphasenwinkel
Ohne Berücksichtigung der Nullphasenwinkel wird ein beliebiger Strom als Referenz genommen.
Daher bleibt der resultierende Strom betragsmäßig gleich, die Phase ändert sich hingegen zu:
Lösung:
siehe Lösungsweg