Aufgabenstellung:
Eine massive Halbkugelschale mit der Leitfähigkeit
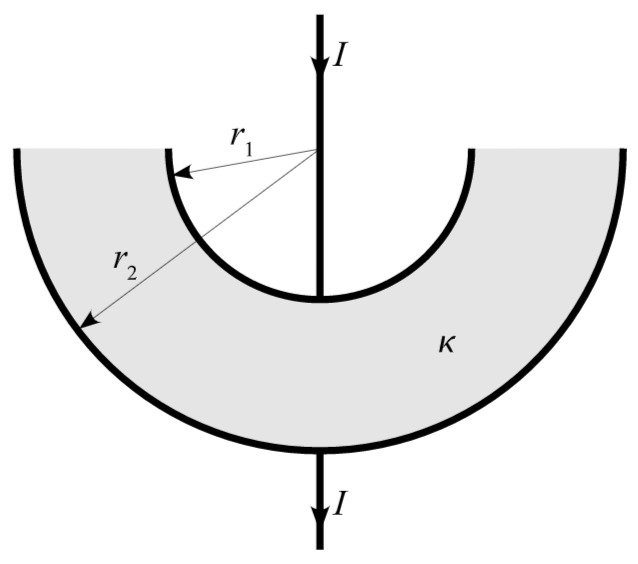
a) Berechnen Sie den Strom
b) Berechnen Sie die elektrische Feldstärke
c) Berechnen Sie die Spannung
d) Berechnen Sie die Spannung
e) Berechnen Sie den elektrischen Widerstand
f) Berechnen Sie den elektrischen Widerstand
Hinweis:
Für eine geschlossene Hüllfläche
Lösungsweg:
Allgemein
Legt man um einen stromdurchflossenen Raum eine beliebige Hüllfäche, so gilt ganz allgemein das Hüllintegral
Aufgrund der Kugelsymmetrie der Anordnung kann die Stromdichte nur eine radiale Komponente besitzen (die allerdings nicht auf eine Ebene beschränkt ist, sondern räumlich - aufgrund der Halbkugel - zu verstehen ist)
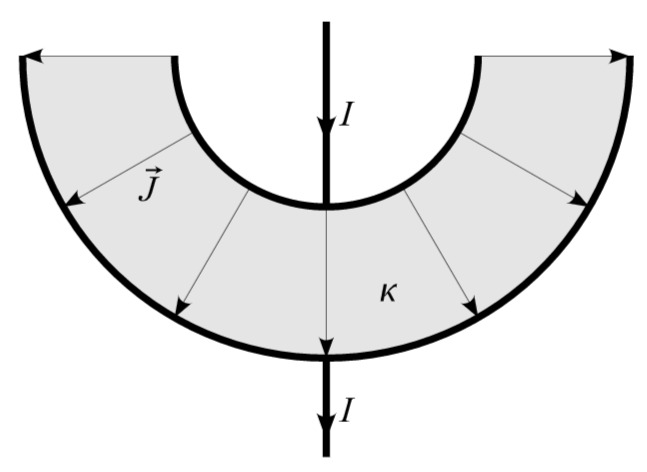
a) Strom
Als Hüllfäche wird eine Halbkugeloberfläche gewählt. Diese Hüllfäche lässt sich in die halbe Kugeloberfläche und die Schnittfläche zerlegen.
Da das Strömungsfeld nur eine radiale Komponente besitzt, liefert das Skalarprodukt nur für die Kugeloberfläche einen von Null verschiedenen Beitrag.
Durch Umstellen erhält man die gesuchte Stromdichteverteilung
b) Feldstärke
Das elektrische Strömungsfeld und die elektrische Feldstärke sind über die spezifische Leitfähigkeit
c) Spannung
Die Spannung
d) Spannung
Zur Bestimmung des Spannungsabfalls zwischen dem Innen- und Außenanschluss muss in Gleichung (1) bzw. (2) für den Radius
e) Widerstand
Den Widerstand der Kugelschale erhält man aus dem Verhältnis des die Schale durchfließenden Stromes
f) Widerstand
Bei der Grenzwertbetrachtung ist es bemerkenswert, dass der Widerstand der Anordnung einen endlichen Wert annimmt, wenn der Außenradius über alle Grenzen anwächst.
Lösung:
a)
b)
c)
d)
e)
f)