Aufgabenstellung:
In einem Koaxialkabel ist der Bereich zwischen Innen- und Außenleiter mit leitfähigem Material gefüllt. Der Bereich
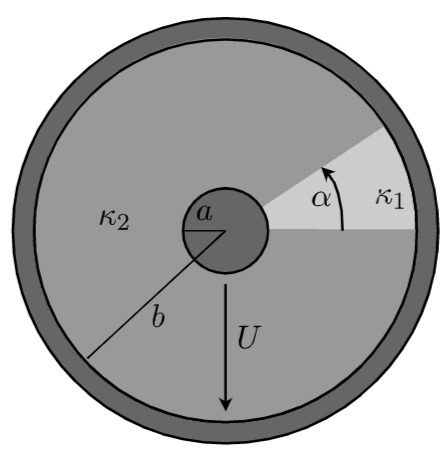
a) Ermitteln Sie den Widerstand zwischen Innen- und Außenleiter für ein Leiterstück der Länge
b) Welche Gesamtleistung
c) Welche Energie wird in Wärme umgewandelt, wenn das Koaxialkabel für einen Zeitabschnitt
Lösungsweg:
a) Widerstand
Den Widerstand erhalten wir aus dem OHM'schen Gesetz.
Wir benötigen den Gesamtstrom
In beiden unterschiedlichen Materialien stellt sich eine radial gerichtete Stromdichte ein.
Die elektrische Feldstärke hat hier nur eine Tangentialkomponente, damit ist die Feldstärke in beiden Materialien gleich groß und ihr Integral ist die Spannung
Den Gesamtstrom für ein Leiterstück der Länge
Aufgelöst nach der elektronischen Feldstärke ergibt sich
Mit
Nun erhalten wir den Widerstand zwischen Innen- und Außenleiter:
b) Gesamtleistung
Die gesamte verbrauchte Leistung berechnet sich mit
Die Leistungsaufteilung zwischen den Materialien entspricht der Stromaufteilung:
c) Wärmeenergie
Nach der Zeit
Lösung:
siehe Lösungsweg