Aufgabenstellung:
Der abgebildete Balken wird am freien Ende durch die im Flächenschwerpunkt angreifenden Kräfte
- Ermitteln Sie die Querschnittsfläche
, den Schwerpunktsabstand die Koordinaten des Schubmittelpunkts, die Flächenträgheitsmomente und im eingezeichneten Koordinatensystem sowie das Torsionsträgheitsmoment und das Torsionswiderstandsmoment . - Ermitteln Sie die Schnittlasten in der Schnittebene, die den Punkt
enthält. - Ermitteln Sie die Spannungen im Punkt
sowie die Hauptspannungen und die Hauptachsen. Stellen Sie den Spannungszustand im Punkt an einem achsenparallelen Rechteck in der -Ebene dar. Zeichnen Sie auch die Hauptachsen ein. - Berechnen Sie die Vergleichsspannung nach der Gestaltänderungshypothese (von Mises) und die Sicherheit
gegen Fließen.
Gegeben:


Lösungsweg:
a) Querschnittskennwerte
Querschnittsfläche:
Schwerpunktsabstand:
Flächenträgheitsmomente:
Torsionsträgheitsmoment und Torsionswiderstandsmoment:
Lage des Schubmittelpunkts:
Schubfluss und Querkraft erzeugen das gleiche Moment bezüglich Punkt

Schubfluss im Abschnitt
Moment des Schubflusses:
Moment der Querkraft:
Aus
Zahlenwerte:
b) Schnittlasten

Zahlenwerte:
c) Spannungszustand im Punkt
Normalspannung
Normalkraft und Biegemomente resultieren aus der Normalspannung
Mit
Zahlenwert:
Schubspannung
Schubspannung infolge der Querkraft
Zur Berechnung der Schubspannung infolge der Querkraft wird das statische Moment des halben Querschnitts benötigt:
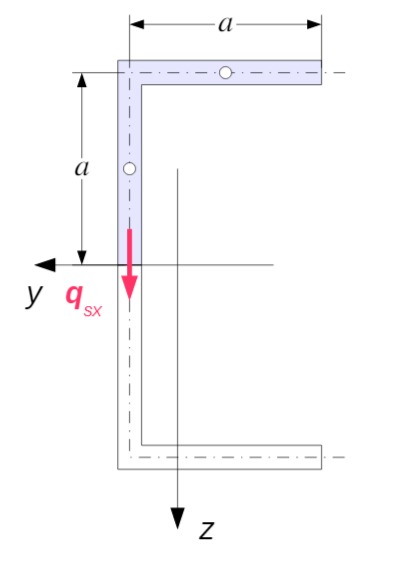
Zahlenwert:
Für die Schubspannung infolge der Torsion gilt:
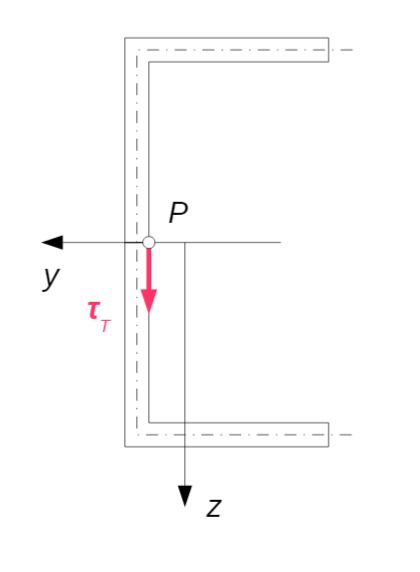
Zahlenwert:
Im Punkt
Zahlenwert:
Hauptspannungen
Mit
Hauptrichtungen:
Mohrscher Spannungskreis (zur Kontrolle) und Spannungen am Rechteck:
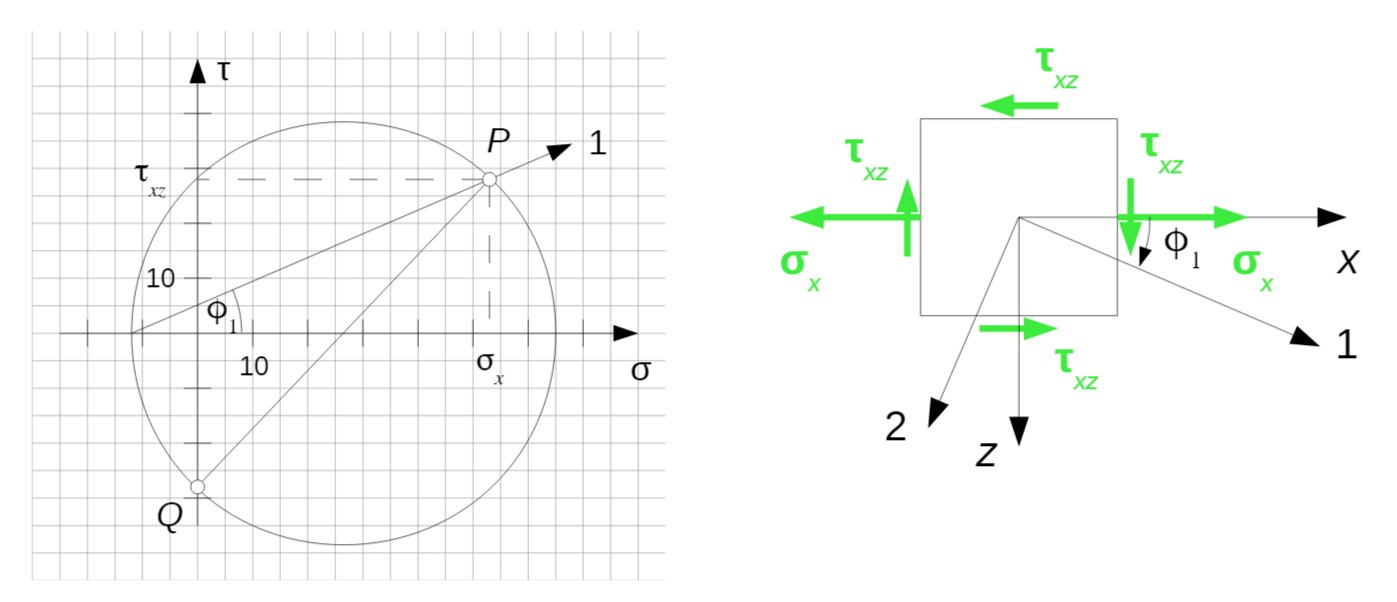
d) Vergleichsspannung und Sicherheit gegen Fließen
Vergleichsspannung nach der Gestaltänderungshypothese:
Zahlenwert:
Sicherheit gegen Fließen:
