Aufgabenstellung:
Bestimmen Sie sämtliche Nullstellen der periodischen Funktion
- unter Verwendung des Additionstheorems der Kosinusfunktion,
- mit Hilfe des Zeigerdiagramms.
Hinweis zu b): Fassen Sie die beiden Summanden als gleichfrequente (mechanische) Schwingungen auf
Lösungsweg:
a) Nullstellen über Additionstheoreme:
Setze
Nutze die Substitution:
Mit dem Additionstheorem der Kosinusfunktion erhalten wir:
(unter Verwendung der trigonometrischen Beziehung
Die Lösungen der Gleichung
Diese lassen sich auch in einer Skizze verdeutlichen:

Lösung im Periodenintervall
Weitere Lösungen liegen im Abstand von ganzzahligen Vielfachen der Periode
Durch Rücksubstitution erhalten wir die gesuchten Nullstellen
b) Nullstellen mit Hilfe des Zeigerdiagramms
Die gleichfrequenten Einzelschwingungen
Zunächst müssen wir die Kosinusschwingung

Drehwinkel:
Auf die Berechnung der Amplitude
Berechnung des Nullphasenwinkels
Mit
Aus dem Zeigerdiagramm entnehmen wir, dass der resultierende Zeiger im 4. Quadranten liegt (Skizze). Somit ergibt sich für
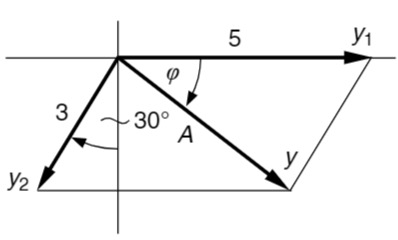
Resultierende Schwingung:
Die Nullstellen der Funktion
Lösung:
Beide Teilaufgaben liefern: