5 / 9

Aufgabenstellung:

Strophoide: mit )

  1. Beschreiben Sie diese Kurve durch explizite Funktionen (in kartesischen Koordinaten) und zeichnen Sie den Kurvenverlauf für den Parameterwert .
  2. Bringen Sie die Kurvengleichung in die Polarkoordinatenform und bestimmen Sie den zulässigen Winkelbereich (im Intervall .

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Wir lösen die Kurvengleichung nach auf und erhalten zwei Funktionen, die durch Spiegelung an der -Achse ineinander übergehen:

Umformungen: Bruch mit erweitern, dann Teilwurzel ziehen.
Kurvenverlauf (für : siehe Skizze

Skizze

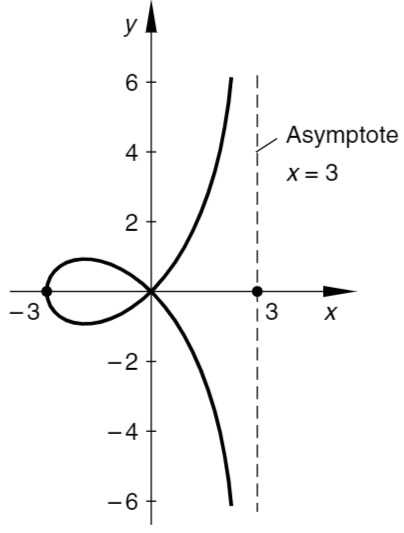
Abbildung

Wertetabelle:

Wir erstellen eine Wertetabelle für die Funktion

b) Kurvengleichung in Polarkoordinaten

Unter Verwendung der Transformationsgleichungen und folgt:

(unter Verwendung der Formeln:

Bestimmung des Definitionsbereiches (Winkelbereiches)

Wir wissen bereits, dass die Kurve spiegelsymmetrisch zur -Achse verläuft, können uns daher bei den weiteren Untersuchungen auf den und Quadranten beschränken. Wegen der Bedingung und da nach Voraussetzung ist müssen und unterschiedliche Vorzeichen haben. Wir unterteilen den Winkelbereich in vier gleiche Teilbereiche, in denen und folgende Vorzeichen besitzen:

Somit sind nur Winkel zwischen und bzw. zwischen und zulässig wegen . Für die Gesamtkurve ergibt sich daher wegen der Spiegelsymmetrie zur -Achse der folgende

Definitionsbereich: .

Lösung:

  2.