Aufgabenstellung:
Bestimmen Sie die Gleichung einer Kurve mit den folgenden Eigenschaften: Ist
- in kartesischen Koordinaten (in impliziter Form)
- in Polarkoordinaten
- Skizzieren Sie den Kurvenverlauf für
Lösungsweg:
Wir wählen das kartesische Koordinatensystem so, dass die Punkte
Skizze
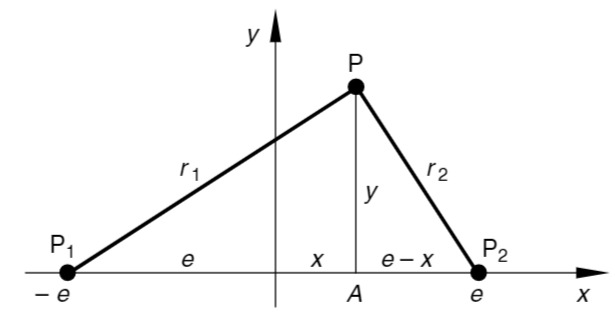
Die Punkte
a)
Die Kurvenpunkte erfüllen die Bedingung
und
Aus der Bedingung
b)
Mit Hilfe der Transformationsgleichungen
(unter Verwendung der trigonometrischen Beziehung
c) Kurvenverlauf für
Skizze
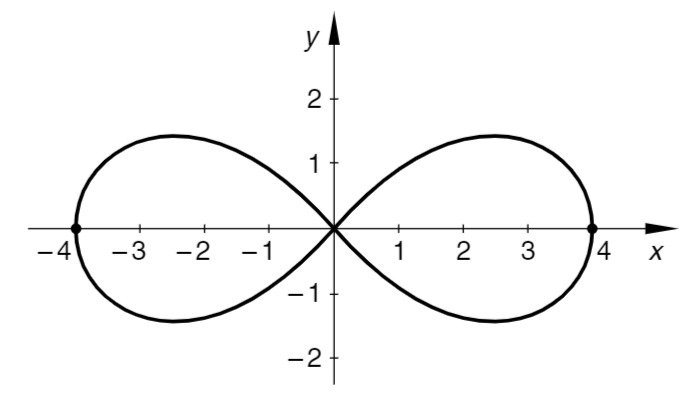
Kurvengleichung in Polarkoordinaten:
Wir müssen die Winkelbereiche von
Wertetabelle: