Aufgabenstellung:
Gegeben ist folgendes Blockschaltbild:
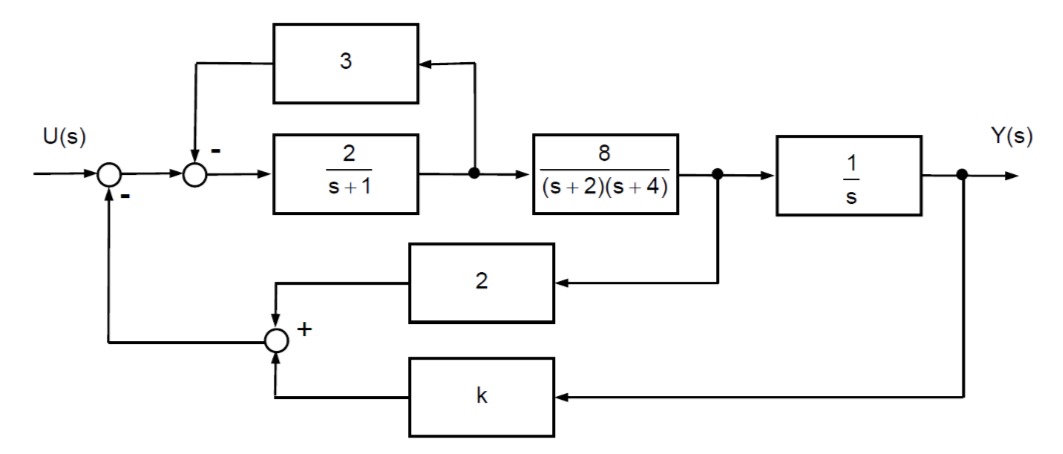
- Bestimmen Sie die Übertragungsfunktion
in Abhängigkeit des Parameters - Ermitteln Sie mit Hilfe des Hurwitz-Kriteriums den Bereich
von , für den das System asymptotisch stabil ist. - Bestimmen Sie den stationären Endwert
für den Fall und . Was lässt sich für den Fall bezüglich aussagen?
Lösungsweg:
a) Übertragungsfunktion
Durch geschicktes Verschieben eines Verzweigungspunktes sowie Zusammenfassen der Rückkopplung im Vorwärtszweig ergibt sich
Durch Umformung ergibt sich dann die gesuchte Übertragungsfunktion
b) Bereich
Zur Bestimmung des Bereiches von
Nach Hurwitz ist die Übertragungsfunktion dann stabil, wenn alle Koeffizenten von
Somit muss für Stabilität
Zusätzlich müssen noch die Determinanten der drei Hurwitz-Matrizen betrachtet werden.
Für die Determinante von
Für die Determinante von
Diese Determiante ist auch unabhängig von
Abschließend wird noch die Determinante von
Durch diese Determinante ergibt sich eine zusätzliche Bedingung für
Somit ergibt sich für
in dem die Übertragungsfunktion stabil ist.
c) Stationärer Endwert
Es gilt für
Somit gilt für den stationären Endwert
Setzt man die Übertragungsfunktion
Somit ergibt sich der stationäre Endwert für den Fall
Für den Fall