Aufgabenstellung:

In einem Zylinder ist unter einem Kolben (Masse vernachlässigbar; Querschnittsfläche
Eine Person drückt nun mit der Hand den Kolben nach unten, bis die Kraft, die sie ausüben muss, auf
In diesem Kräftegleichgewicht, herrscht nun im Gas der Druck
-
Bestimmen Sie den Druck
und die Kolbenhöhe . -
Welche Temperatur
stellt sich ein? -
Auf welche Höhe
sinkt der Kolben? -
Welche Stoffmenge
ist im Zylinder eingeschlossen? -
Welche Arbeit
wird bei der ersten Kompression ( auf ), welche Arbeit bei der zweiten Kompression ( auf ) und welche Arbeit insgesamt am Gas verrichtet?
Lösungsweg:
Vorbemerkung
Die beiden Zustandsänderungen des Gases sind
- '1' → '2' : Isentrope Kompression,
- '2' → '3' : Isobare Kompression.
Grafische Darstellung im
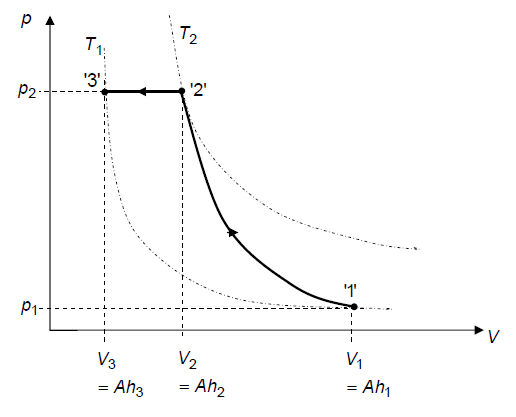
(a) Bestimmung von Druck
Da sich alle Prozesse in einem Zylinder abspielen, ist das Volumen stets proportional zur Kolbenhöhe und immer darstellbar als
Der Druck
Der Isentropenexponent
Daraus ergibt sich der Isentropenexponent
Die Isentropengleichung, die Drücke und Volumina miteinander verknüpft, lautet
Also
(b) Temperatur
Die Zustandsgleichung verknüpft die Zustandsgrößen
daraus ergibt sich
Damit
Alternative
Man bestimmt zunächst die Stoffmenge
(c) Höhe
Für den isobaren Prozess '2'
Oder
mit der Zusatzforderung
erhält man
(d) Stoffmenge
Die Zustandsgleichung eines idealen Gases für den Zustand '1' liefert die Stoffmenge
(e)
Für die verrichtete Arbeit beim isentropen Prozess '1'
Die molare isochore Wärmekapazität
Damit
Für die umgesetzte Arbeit beim isobaren Prozess ' 2 '
Damit wird die insgesamt umgesetzte Arbeit
Lösung:
-
bar -
-
-
-