Aufgabenstellung:
Ein vertikaler Zylinder mit einer Querschnittsfläche von
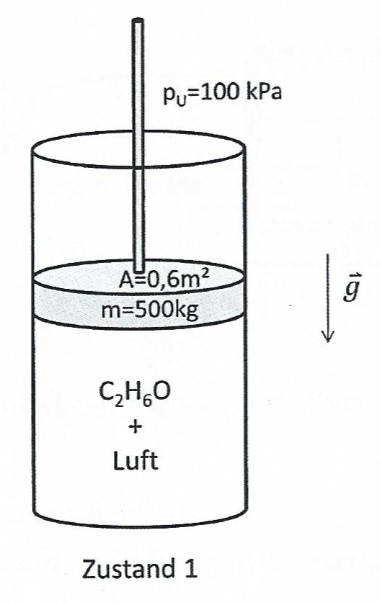
-
Bestimmen Sie den Druck
im Zylinder.
Wenn Sie den Aufgabenteil nicht lösen können, rechnen Sie bitte mitweiter. -
Berechnen Sie das Volumen
sowie die an die Umgebung abgegebene Wärme .
Annahmen:
- Die Standardbildungsenthalpie von gasförmigem Ethanøl beträgt
. - Die Differenz der molaren Enthalpien von Ethanol im idealen Gaszustand zwischen
und beträgt . - Alle gasförmigen Komponenten sollen als ideale Gase bzw. ideale Gasgemische/betrachtet werden.
- Die Erdbeschleunigung beträgt
. - Änderungen der äußeren Energien sind zu vernachlässigen.
Lösungsweg:
a) Druck
Es wird ein Kräftegleichgewicht am Kolben aufgestellt um den gesuchten Druck zu bestimmen:
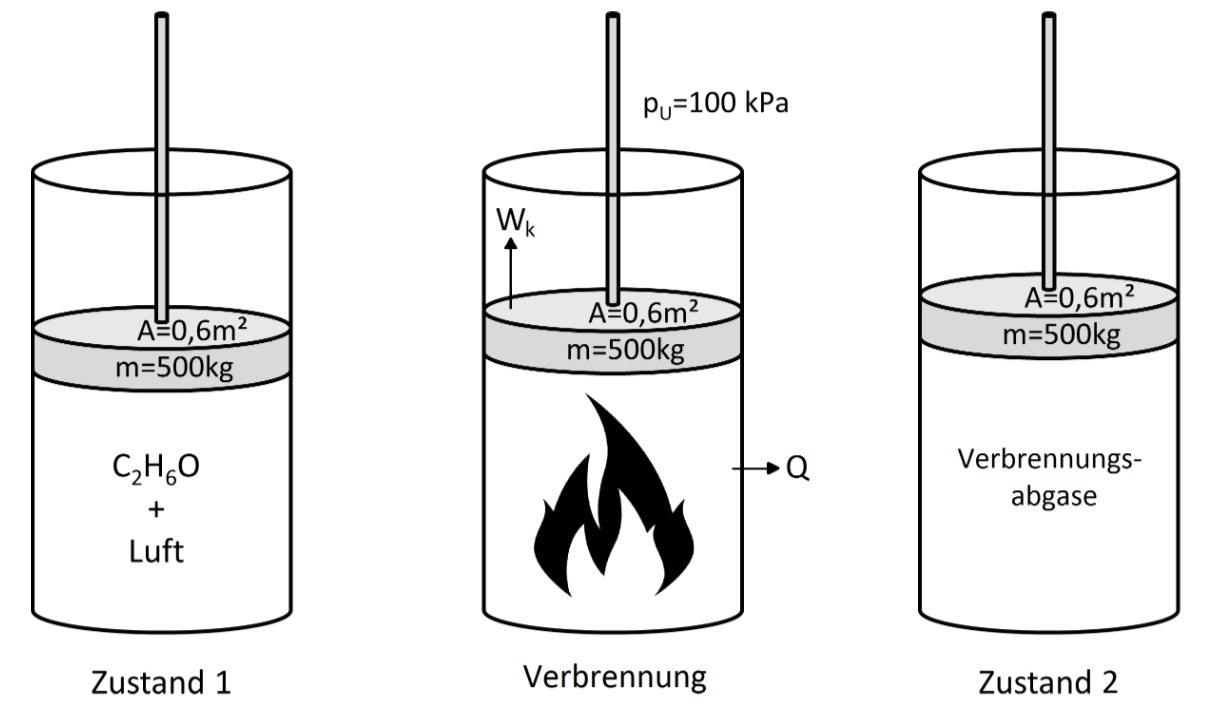
b) Volumen
Zur Bestimmung von
Bei der Verbrennung entsteht kein flüssiges Wasser, weil die vorliegende Temperatur über der Siedetemperatur bei vorliegendem Druck liegt. Die stöchiometrische Verbrennung wird durch folgende Reaktionsgleichung dargestellt:
Zunächst muss die Stoffmenge der eingesetzten Edukte bestimmt werden. Hierzu wird das ideale Gasgesetz angewendet:
Die Stoffmenge des Brennstoffs lässt sich dann wie folgt berechnen:
Nun kann
Zur Bestimmung der Wärmemenge wird eine Energiebilanz um das Fluid im Kolben aufgestellt (geschlossenes System) und diese integriert:
Es gilt
Da der Innendruck konstant bleibt, lässt sich die Energiebilanz folgendermaßen umformen:
Da
Es sind nun alle erforderlichen Größen für die Energiebilanz bekannt und die Wärme kann berechnet werden: