Aufgabenstellung:
Ein Bügelsystem besteht aus einem Dampfbügeleisen und einem beheizbaren Wassertank. Der Wassertank ist zylindrisch und besitzt bei einem Durchmesser von
Bei Beginn des Bügelprozesses (Zustand 1) wird das Regelventil des Dampfbügeleisens geöffnet, wodurch gesättigter Wasserdampfyaus dem Wassertank austritt. Der Druck im Wassertank beträgt
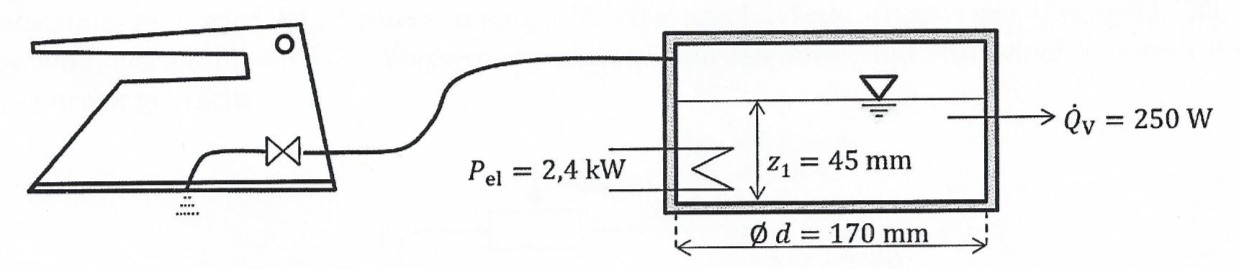
Bestimmen Sie die Zeitspanne
Annahmen:
- Das Ventil und der Schlauch sind adiabat.
- Der Heizer ist in jedem Zustand vollständig in Wasser getaucht.
- Der Druck im Wassertank bleibt zwischen Zustand 1 und Zustand 2 konstant.
- Im Wassertank befinden sich nur flüssiges Wasser und Wasserdampf, die zu jedem Zeitpunkt im Gleichgewichty stehen.
- Änderungen der äußeren Energien sind zu vernachlässigen.
Lösungsweg:
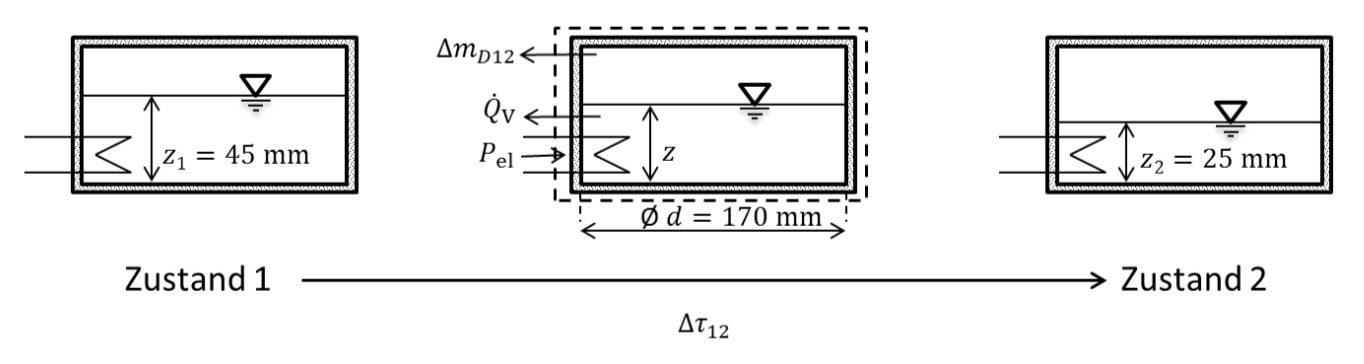
Die Zeitspanne
Integration liefert:
Die Gesamtmasse des Wassers im Zustand 1 ergibt sich aus der Summe des gasförmigen und des flüssigen Wassers:
Man bestimmt die Masse des flüssigen Wassers über das Volumen des Füllstands:
Mit Hilfe des spezifischen Volumens aus einer Tabelle zum Sättigungszustand
ergibt sich die Masse des flüssigen Wassers zu:
Für das Volumen des gasförmigen Wassers gilt:
Mit dem spezifischen Volumen des gasförmigen Wassers aus einer Tabelle zum Sättigungszustand
kann die Masse des gasförmigen Wassers berechnet werden:
Durch Einsetzen der notwendigen Zahlenwerte ergibt sich die Gesamtmasse des Wassers im Zustand 1 zu:
Die Gesamtmasse des Wassers im Zustand 2 kann aus folgender Massenbilanz bestimmt werden:
Die ausgetretene Dampfmasse
Das verdampfte Volumen
Durch Einsetzen der notwendigen Zahlenwerte ergibt sich die Gesamtmasse im Zustand 2 zu:
Der Dampfgehalt im Zustand 2 ,
wird genutzt, um die spezifische innere Energie im Zustand 2 zu berechnen. Die spezifischen inneren Energien werden aus einer Tabelle zum Sättigungsdampfdruck entnommen:
Damit ergibt sich die innere Energie im Zustand 2 zu:
Zudem muss der Dampfgehalt
Damit ergibt sich die innere Energie im Zustand 1 zu:
Die noch fehlende Größe
Somit ergibt sich die gesuchte Zeit