Aufgabenstellung:
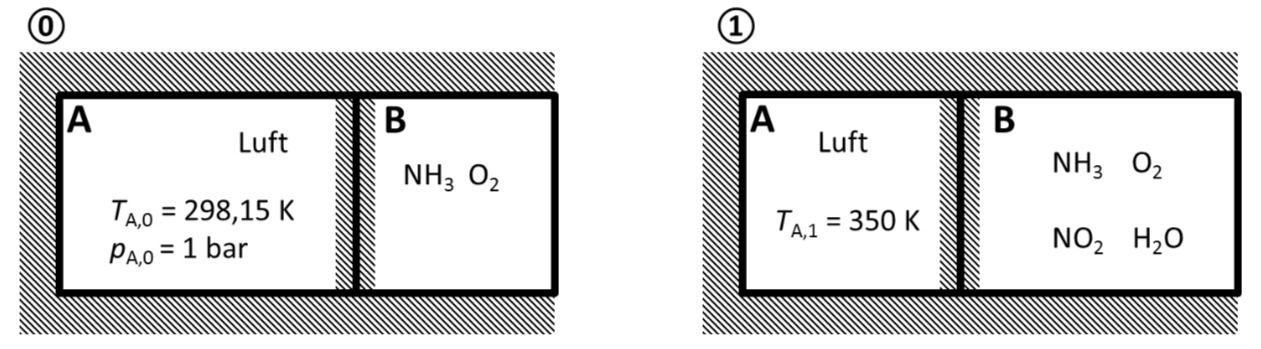
Es wird ein liegender Zylinder betrachtet, in dem ein adiabater, reibungsfrei gelagerter Kolben zwei Kammern (A und B) voneinander trennt. Im Zustand 0 befinden sich in Kammer B Ammoniak
Im Zustand 1 liegt in Kammer B ein Reaktionsgleichwicht von
Für
Annahmen:
- Alle Gase und Gasgemische sind ideal.
- Die Wärmekapazität von Luft ist über den betrachteten Temperaturbereich konstant.
- Die Reaktionsenthalpie ist über den betrachteten Temperaturbereich konstant.
- Der Kolben sowie Kammer A sind adiabat.
- Die Änderung von Zustand 0 zu Zustand 1 verläuft in Kammer A reibungsfrei.
- Änderungen der äußeren Energien sind zu vernachlässigen.
- Bestimmen Sie die Gleichgewichtszusammensetzung in Kammer B zum Zustand 1.
Wenn Sie den Aufgabenteil nicht lösen können, rechnen Sie bitte mit, weiter. - Bestimmen Sie die Temperatur
in Kammer B zum Zustand 1.
Lösungsweg:
a) Gleichgewichtszusammensetzung in Kammer B zum Zustand 1
Die Bruttoreaktionsgleichung für die Reaktion von
Der Stoffmengenanteil einer Komponente
Die Umsatzvariable berechnet sich mit Hilfe des Umsatzes.
Die gegebenen Informationen lassen sich tabellarisch darstellen.
b) Temperatur
Zunächst bestimmen wir den Druck
Da der Kolben reibungsfrei gelagert ist, besteht ein Kräftegleichgewicht zwischen Kammer A und Kammer B. Es gilt also:
Darüber hinaus sind Kolben und Kammer A adiabat, und die Zustandsänderung von 0 nach 1 verläuft reibungsfrei. Daher ist die Zustandänderung von 0 nach 1 in Kammer A isentrop. Da wir den Druck
Da die Gleichgewichtszusammensetzung und der Druck
Wird
Wir können annehmen, dass die Reaktionsenthalpie
Mit den alternativen Stoffmengenanteilen ergibt sich in Kammer B eine Temperatur von