Aufgabenstellung:
Zur Verringerung des Kohlenstoffmonoxid-Anteils in einem Gasgemisch wird die WassergasKonvertierungsreaktion genutzt. Diese Reaktion läuft gemäß der Reaktionsgleichung
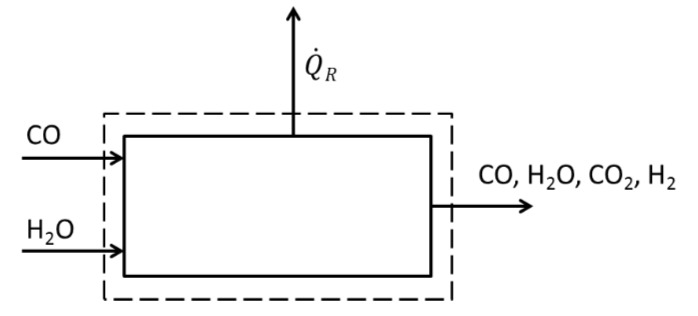
ab. Einem isothermen Reaktor
-
Berechnen Sie die Gleichgewichtskonstante
der Reaktion bei den im Reaktor vorliegenden Bedingungen.
Wenn Sie den Aufgabenteil nicht lösen können, rechnen Sie bitte mitweiter. -
Berechnen Sie die Umsatzvariable
sowie die Stoffmengenanteile im Produktstrom.
Wenn Sie den Aufgabenteil nicht lösen können, rechnen Sie bitte mit, weiter. -
Bestimmen Sie, ob dem Reaktor ein Wärmestrom zu- oder abgeführt werden muss. Berechnen Sie den zu- oder abgeführten Wärmestrom.
Annahmen:
- Edukt- und Produktstrom können als ideale Gasgemische betrachtet werden.
- Eduktströme sind bereits beim Eintritt in den Reaktor auf Reaktionstemperatur.
- Änderungen der äußeren Energien sind zu vernachlässigen.
Lösungsweg:
a) Gleichgewichtskonstante K
Da es sich um eine isotherme Reaktion bei einer konstanten Reaktionstemperatur von
Dabei gilt für das chemische Potential
Da es sich um ideale Gasgemische handelt, ist
Dabei sind die Reaktionsenthalpie
Die Berechnung von Reaktionsenthalpie und Reaktionsentropie sind im Folgenden in Form von Tabellen dargestellt. Für die Reaktionsenthalpie ergibt sich mit den Werten aus Stoffwerttabellen zu Enthalpiezuständen für
Die Reaktionsentropie
Die Gleichgewichtskonstante
b) Umsatzvariable
Die Gleichgewichtszusammensetzungen
Über das Massenwirkungsgesetz ergibt sich eine Bestimmungsgleichung für
Dieser Ausdruck für
Aus der obigen Tabelle lässt sich an den aufgeführten Gleichungen zur Beschreibung der Gleichgewichtszusammensetzung erkennen, dass physikalisch relevante Lösungen für
Eingesetzt in die obige Tabelle ergibt sich für die Gleichgewichtszusammensetzung
c) zu- oder abgeführter Wärmestrom:
Die Berechnung des zu- oder abgeführten Wärmestroms kann durch eine Energiebilanz um den Reaktor erfolgen. Laut Aufgabenstellung handelt es sich um einen isothermen Reaktor. Im Zuge der Lösung zur Berechnung der Gleichgewichtskonstanten
mit
Mit der zuvor bestimmten, molaren Reaktionsenthalpie