4 / 8

Aufgabenstellung:

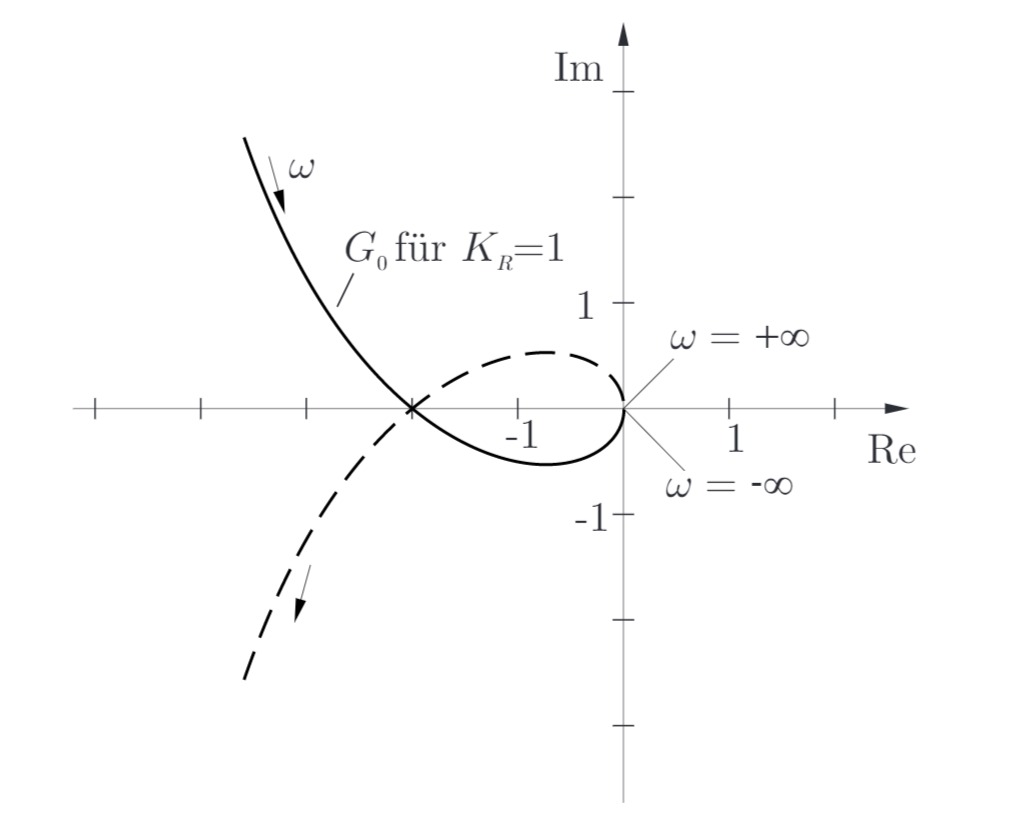
Abbildung

Die Regelstrecke soll mit einem -Regler mit Verstärkung geregelt werden. Die Ortskurve von ist für abgebildet. Für die Systemmatrix der Zustandsraumdarstellung von gilt

mit dem unbekannten Parameter .

  1. Bestimmen Sie die Eigenwerte von und anschließend den Parameter mithilfe der Ortskurve.
  2. Ergänzen Sie die Ortskurve zu einer geschlossenen Kurve, um die Anwendung des Nyquist-Kriteriums zu ermöglichen.
  3. Ermitteln Sie den Parameterbereich von , für welchen der geschlossene Regelkreis stabil ist.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Eigenwerte von und Parameter

Bei handelt es sich um eine obere Dreiecksmatrix. Daher sind ihre Eigenwerte und die Elemente auf der Hauptdiagonalen.

Da die Ortskurve aus dem Unendlichen kommt, besitzt das System eine Polstelle bei , dadurch lässt sich auf schließen.

b) Ergänzen Sie die Ortskurve zu einer geschlossenen Kurve

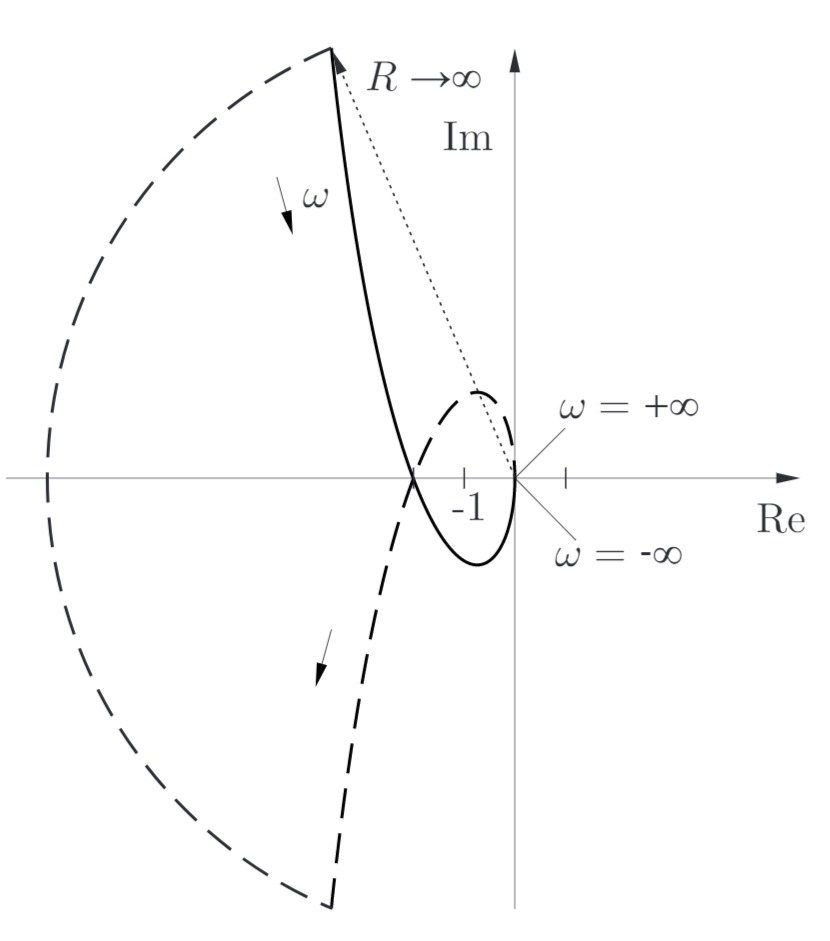
Abbildung

Hinweis: In der -Ebene muss die im Ursprung liegende Polstelle von der Nyquistkontur  umgangen werden, was durch einen Halbkreis mit infinitesimalem Radius in der rechten Halbebene geschehen kann, sodass der Integratorpol in Durchlaufrichtung links von der Nyquistkontur liegt.
Aus der Orientierungserhaltung der Abbildung folgt, dass das im Unendlichen liegende Bild des Integratorpols in der -Ebene ebenfalls in Durchlaufrichtung links von der vervollständigten Ortskurve liegen muss. Der Kreisbogen mit gegen Unendlich strebendem Radius, der die Ortskurve zwischen und schließt, muss damit im mathematisch negativen Sinn durchlaufen werden und somit in der linken Halbebene liegen.

c) Parameterbereich von

Mit liefert das vollständige Nyquist-Kriterium die Bedingung um Stabilität des geschlossenen Regelkreises sicherzustellen.

Ablesen der Umdrehungen entgegen dem mathematisch positiven Sinn um den kritischen Punkt:

üüü

Lösung:

  1. und ;  
  2. siehe Musterlösung