3 / 20

by Manfred Strohrmann

(H.ErT.Z-Online)

Aufgabenstellung:

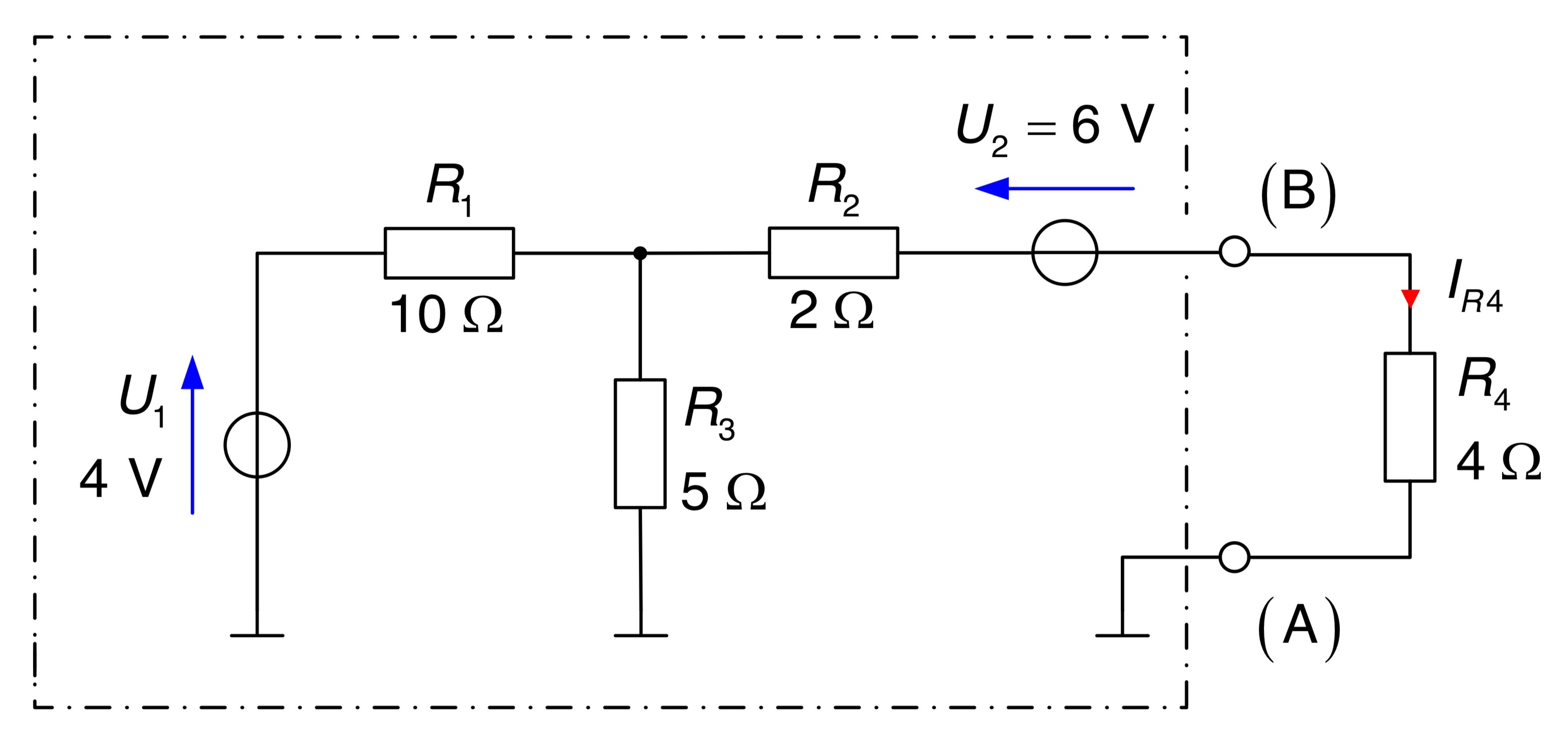
In der folgenden Schaltung ist ein Zweipol, markiert durch den gestrichelten Bereich, mit den Klemmen (A) und (B) dargestellt.

Ermitteln Sie das Ersatzschaltbild des Zweipols an den Klemmen (A) - (B) mit Hilfe

  1. von Maschen- und Knotensatz.
  2. des Superpositionsprinzips.
  3. Berechnen Sie des Weiteren den Strom und die Spannung

Abbildung

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Bestimmen des Ersatzschaltbildes durch Maschen- und Knotensatz

Bei der Ermittlung des Ersatzschaltbildes mit Hilfe der Kirchhoffschen Regeln macht es noch vor Beginn einer Berechnung Sinn, sich Gedanken zur grundsätzlichen Vorgehensweise zu machen.

Gesucht ist eine Ersatzspannungsquelle mit den Größen und .

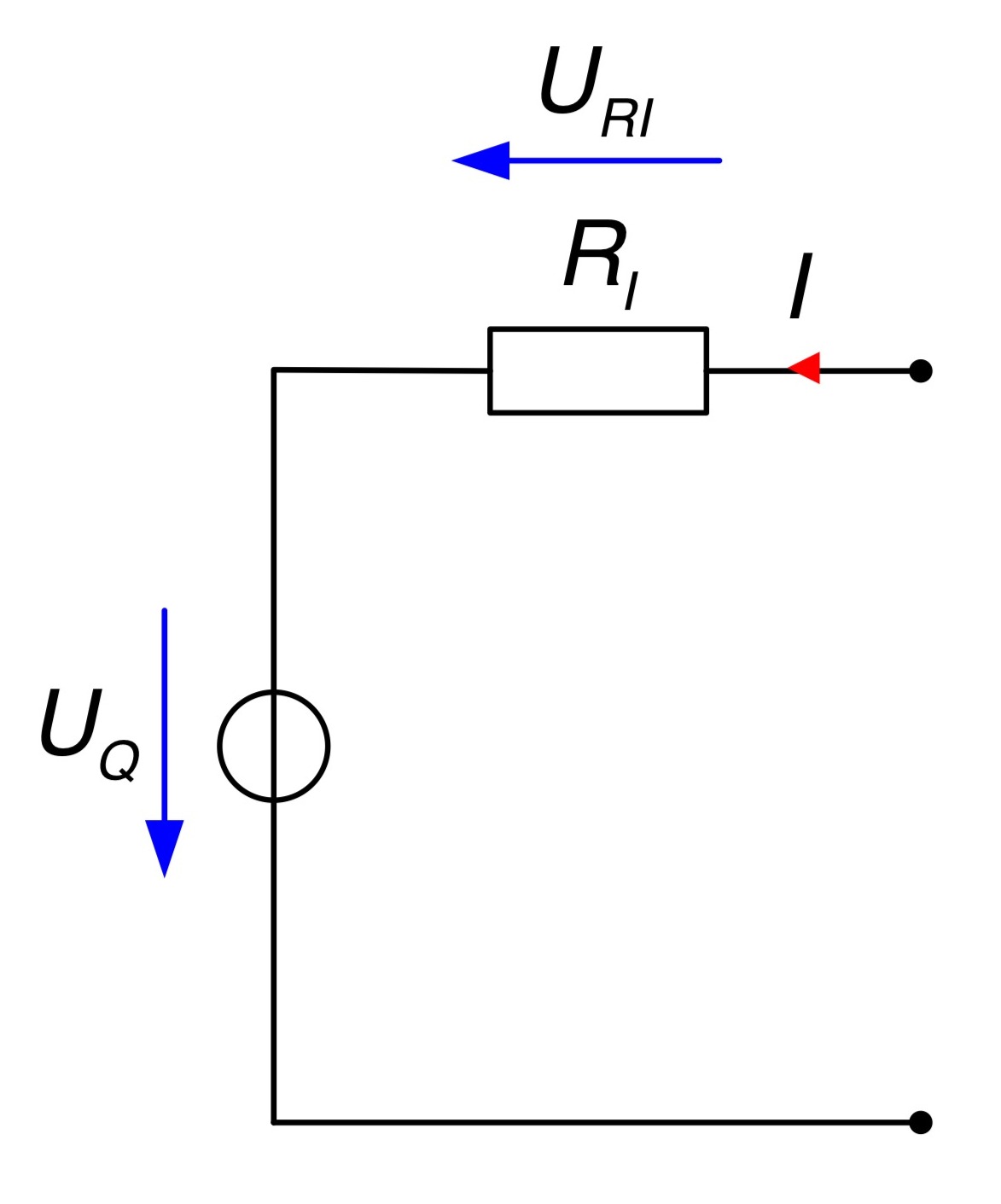
Die nebenstehende Schaltung zeigt eine lineare Spannungsquelle.

 

Die zugehörige Gleichung lautet:

 

Abbildung

Um die Größen und bestimmen zu können, muss mit Hilfe der Kirchhoffschen Regeln eine Gleichung, entsprechend der Form einer linearen Spannungsquelle, aufgestellt werden.

Zunächst werden alle Spannungen und Ströme mit Zählpfeilen versehen.

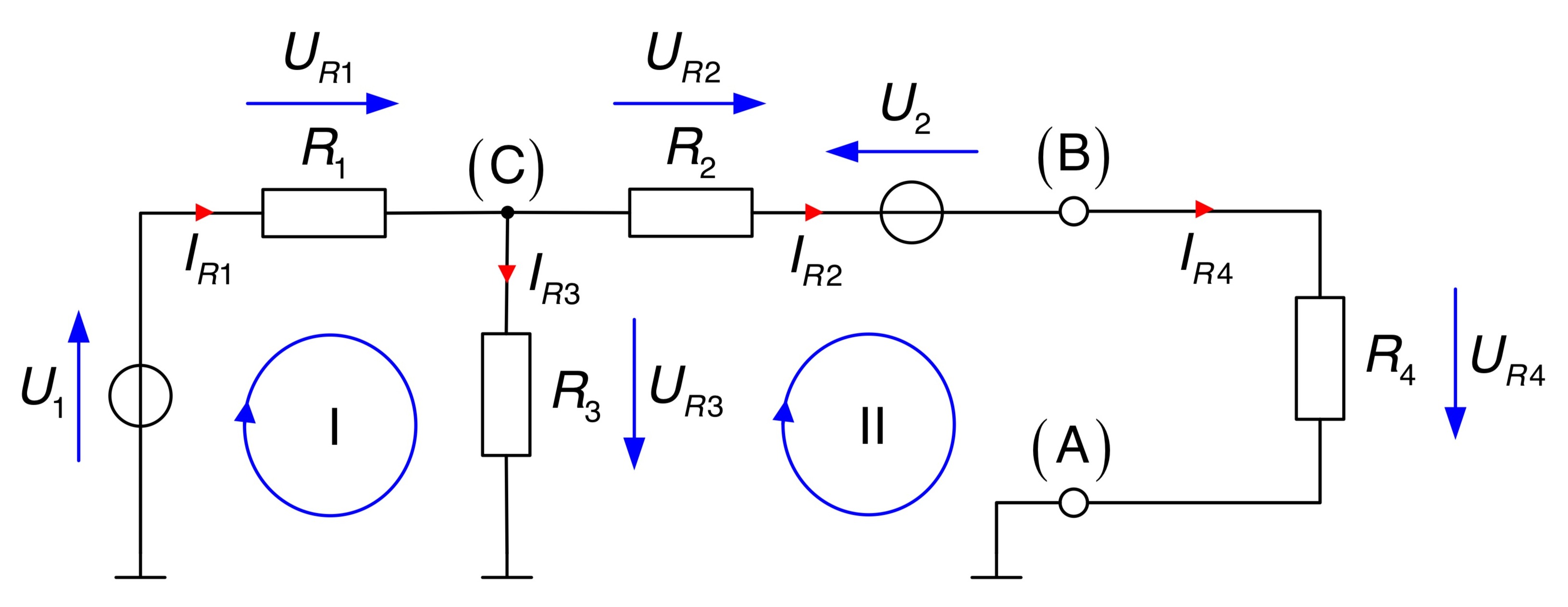
Abbildung

Der Knoten, an dem die Widerstände und zusammengeschaltet sind, wird als Knoten (C) bezeichnet.

Es gilt der Zusammenhang

Des Weiteren können zwei Maschengleichungen aufgestellt werden.

Masche I ergibt sich zu

und Masche II entsprechend zu

Die Ströme und werden in der Knotengleichung durch das ohmsche Gesetz ersetzt.

Daraus ergibt sich für die Knotengleichung

Die Spannung wird durch die erste Maschengleichung ersetzt.

Der Strom ist identisch zum Strom und kann diesen ersetzen.

Nach Einsetzen von und einigen Umformungen lautet die Gleichung

Mit Hilfe der zweiten Maschengleichung kann die Spannung ersetzt werden.

Die Spannung am Widerstand wird mit Hilfe des ohmschen Gesetzes ausgedruickt.

Ausmultiplizieren und nach der Spannung auflösen ergibt

Diese Form entspricht der Grundgleichung linearer Spannungsquellen.

Durch einen Koeffizientenvergleich können die Größen und ermittelt werden.

Die Lösung über Maschen- und Knotengleichungen ist aufwändig und unübersichtlich.

b) Bestimmen des Ersatzschaltbildes durch Superposition

Zum Errechnen des Innenwiderstandes werden alle Spannungsquellen kurzgeschlossen.

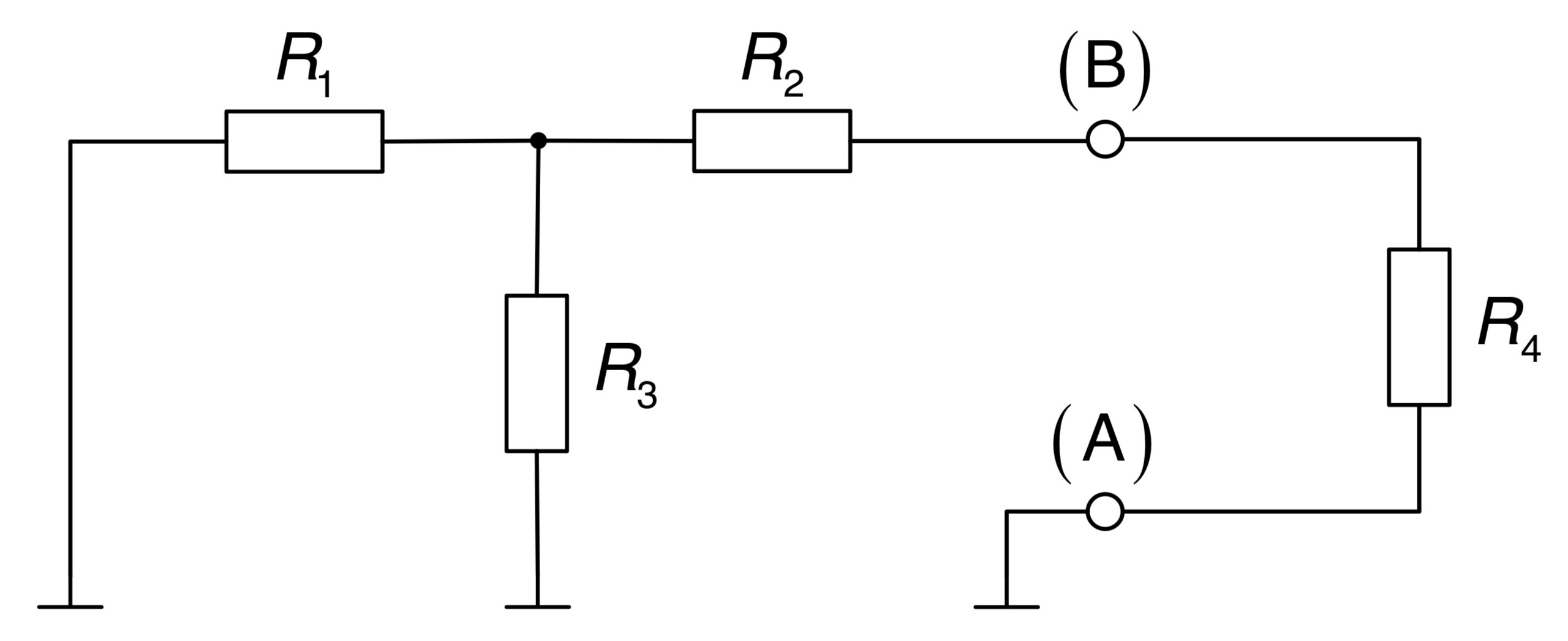
Abbildung

Damit ergibt sich eine Schaltung, bestehend aus Reihen- und Parallelschaltung, die zusammengefasst wird zu

Da die Leerlaufspannung bestimmt werden soll, gilt für den Widerstand dass dieser nicht angeschlossen ist.

Der Strom ist damit gleich null.

Zunächst wird der Beitrag der Quelle bestimmt.

Es gilt

Die Spannung kann über die Spannungsteilerregel angegeben werden.

Wird die Quelle zu null gesetzt, fließt durch die Widerstände kein Strom und der Beitrag der Quelle ergibt sich

Die Überlagerung beziehungsweise Superposition der beiden Spannungsanteile liefert das Endergebnis

Beide Lösungswege führen zu dem identischen Ergebnis. Der Weg über das Superpositionsprinzip ist jedoch deutlich weniger umfangreich.

Lösung:

  1. ,
    Fazit: Die Lösung über Maschen- und Knotengleichungen ist aufwändig und unübersichtlich.
  2. Fazit: Beide Lösungswege führen zu dem identischen Ergebnis. Der Weg über das Superpositionsprinzip ist jedoch deutlich weniger umfangreich.
  3. ,