Aufgabenstellung:

Für das dargestellte Rad sind die Masse
Gegeben: Dichte
Lösungsweg:
Die drei Linien durch den Mittelpunkt des Rades und einen der Mittelpunkte der drei Bohrungen sind Symmetrielinien. Daher liegt der Massenschwerpunkt im Mittelpunkt des Rades:
Zur Berechnung der Masse und des Massenträgheitsmoments wird das Rad in sechs Teilkörper unterteilt, nämlich den Radkranz, die Radscheibe, die mittlere Bohrung und die drei sternförmig angeordneten Bohrungen.
Die Gesamtmasse berechnet sich aus der Masse des Radkranzes und der Radscheibe abzüglich der Massen der Bohrungen. Entsprechend berechnet sich das Massenträgheitsmoment aus den Massenträgheitsmomenten des Radkranzes und der Radscheibe abzüglich der Massenträgheitsmomente der Bohrungen.
Radkranz
Der Radkranz ist ein dickwandiger Hohlzylinder (Skizze):
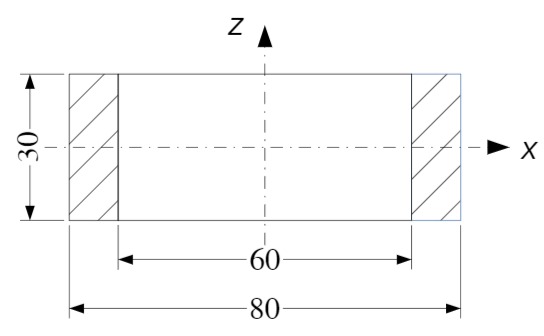
Masse:
Massenträgheitsmoment:
Radscheibe
Die Radscheibe ist ein Zylinder (Skizze)
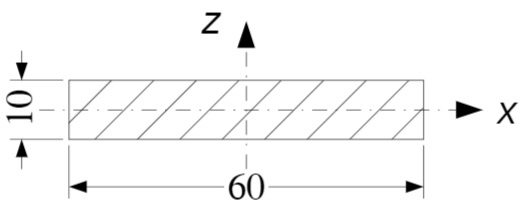
Masse:
Massenträgheitsmoment:
Mittlere Bohrung
Die Bohrung ist ein Zylinder (Skizze)
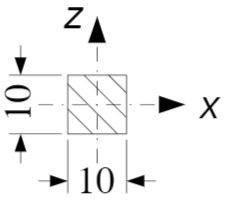
Masse:
Massenträgheitsmoment:
Sternförmige Bohrungen
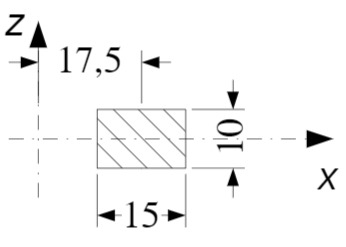
Alle drei Bohrungen sind Zylinder und haben dieselbe Masse und dasselbe Massenträgheitsmoment.
Masse:
Massenträgheitsmoment:
Gesamtes Rad
Masse:
Massenträgheitsmoment: