Aufgabenstellung:
Fahrzeug
Fahrzeug
Wie groß muss die Verzögerung
Gegeben:
Lösungsweg:
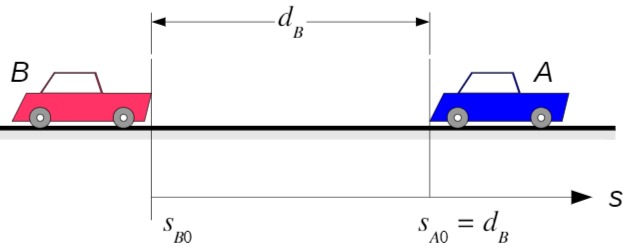
Wahl des Koordinatensystems
Die Zeit wird ab dem Zeitpunkt gemessen, zu dem Fahrzeug
Als Nullpunkt für die Ortskoordinate
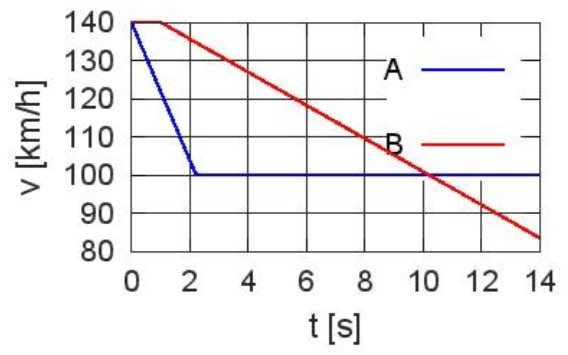
Skizze des Vorgangs im Ort-Zeit-Diagramm
Zum Zeitpunkt
Zum Zeitpunkt
Umrechnung der Geschwindigkeiten auf Meter/Sekunde
Fahrzeug A
Während des Bremsens
Am Ende des Bremsens hat das Fahrzeug die Geschwindigkeit
Daraus folgt für die Bremszeit:
Aus
Zahlenwerte:
Nach dem Bremsen
Fahrzeug
Während der Zeit
Zum Zeitpunkt des Bremsbeginns befindet sich das Fahrzeug an der Stelle
Wegen
Zahlenwerte:
Wegen
Während des Bremsens
Auftreffen von Fahrzeug
Fahrzeug
Aus diesen beiden Gleichungen können die beiden Unbekannten
- Fahrzeug
trifft auf Fahrzeug während beide Fahrzeuge bremsen. - Fahrzeug
trifft auf Fahrzeug während Fahrzeug mit der konstanten Geschwindigkeit fährt.
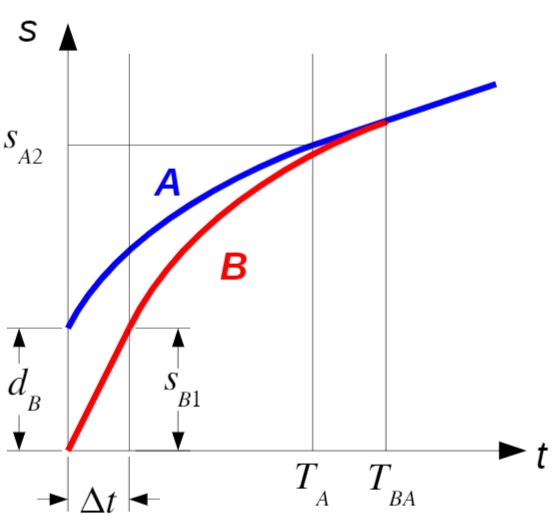
Fall 1: Fahrzeug A bremst
Die beiden Bedingungen dafür, dass Fahrzeug
Aus der ersten Gleichung folgt:
Aus der zweiten Gleichung folgt zunächst
Unter Benutzung der Gleichung für
Zahlenwert und interpretation:
Wegen
Fall 2: Fahrzeug A fährt mit der konstanten Geschwindigkeit
Die beiden Bedingungen dafür, dass Fahrzeug
Aus der ersten Gleichung folgt:
Einsetzen in die zweite Gleichung liefert
Daraus folgt aufgelöst nach
Zahlenwert:
Für die gesuchte Verzögerung
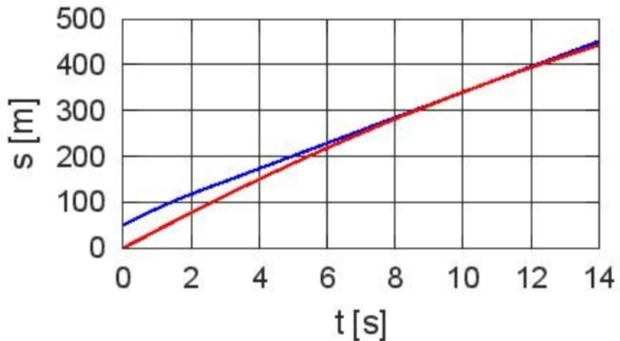
Diagramme