2 / 4

Aufgabenstellung:

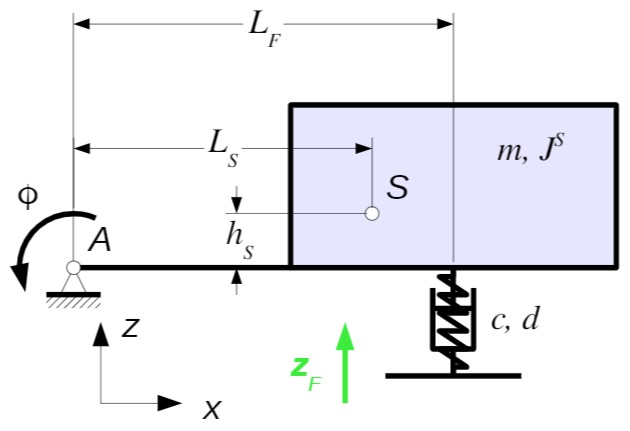AbbildungDas Berechnungsmodell eines einachsigen Anhängers besteht aus einer Masse mit Massenträgheitsmoment bezüglich des Schwerpunkts, einer Feder mit der Federkonstanten und einem Dämpfer mit der Dämpferkonstanten . Die Kupplung wird als Festlager betrachtet.

Die Unebenheit der Fahrbahn wird durch beschrieben. Der Winkel , der die Auslenkung beschreibt, darf als klein angenommen werden.

  1. Ermitteln Sie die Eigenkreisfrequenz und das Lehrsche Dämpfungsmaß .
  2. Geben Sie die Beziehungen an, mit denen sich die Komponenten der Absolutbeschleunigung des Schwerpunkts und der Kraft im Punkt in Abhängigkeit von der konstanten Fahrgeschwindigkeit berechnen lassen.

Gegeben:


Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Schwingungsparameter

Massenträgheitsmoment bezüglich :

Drallsatz bezüglich :

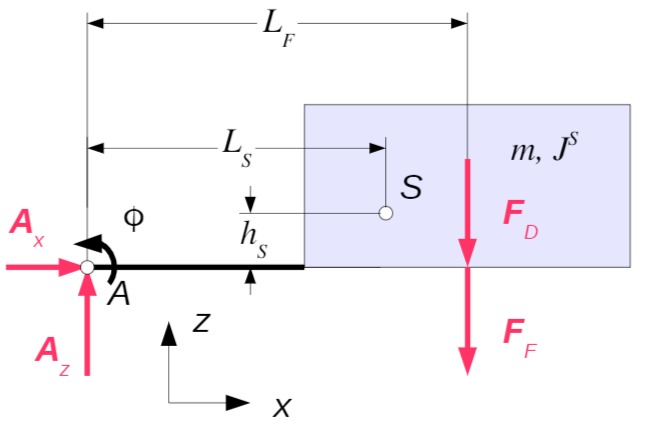
Abbildung

Für kleine Winkel gilt für die Kräfte:

Einsetzen in den Drallsatz ergibt:

Division durch führt auf die Schwingungsgleichung

Daraus kann abgelesen werden:

Zahlenwerte:

b) Beziehungen für Beschleunigungen und Kräfte

Feder- und Dämpferkraft hängen von der Relativbewegung ab. Für kleine Winkel gilt:

Mit gilt:

Wenn das Fahrzeug mit konstanter Geschwindigkeit fährt, gilt: Daraus folgt:

Aus der Schwingungsgleichung folgt:

Damit gilt für den zeitlichen Verlauf des relativen Winkels

mit dem dynamischen Überhöhungsfaktor und dem Phasenwinkel

Der absolute Winkel berechnet sich zu

Für die Winkelbeschleunigung folgt:

Der Schwerpunkt bewegt sich auf einer Kreisbahn mit Radius um Punkt .

Für seine Bahngeschwindigkeit gilt:

Die Bahnbeschleunigung berechnet sich zu

Für die Zentripetalbeschleunigung gilt:

Für die Komponenten der Beschleunigung in - und -Richtung folgt:

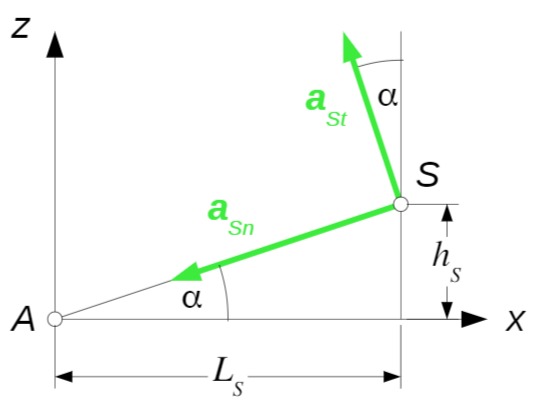
Abbildung

Der Winkel berechnet sich aus

Die Kräfte im Lager können mit dem Schwerpunktsatz berechnet werden:

Dabei gilt für die Dämpferkraft und für die Federkraft

Lösung:

Siehe Lösungsweg.