Aufgabenstellung:
Zwischen den Elektroden eines Kugelkondensators liegt die Spannung
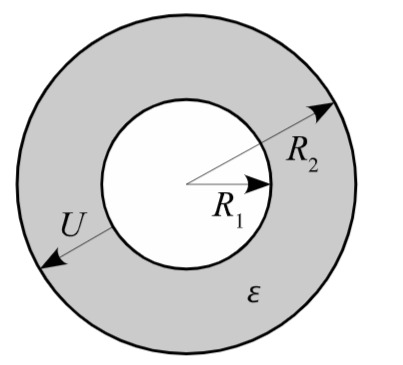
a) Berechnen Sie den Betrag der elektrischen Feldstärke
b) Berechnen Sie die elektrische Energiedichte
c) Berechnen Sie die in dem Kondensator gespeicherte Energie
Lösungsweg:
a) Feldstärke
Zur Berechnung der elektrischen Feldstärke wird das Hüllenintegral herangezogen. Konzentrisch zur Innenelektrode wird eine Hüllfläche gelegt. Aufgrund der Kugelsymmetrie ist der Betrag der elektrischen Feldstärke n jedem Punkt der Hülle gleich groß. Außerdem zeigt der Richtungsvektor der elektrischen Feldstärke
Diese Gleichung lässt sich nach
Die Ladung
Gleichung (2) kann nun nach der Ladung
b) Energiedichte
Für die Energiedichte gilt die Beziehung
Setzt man Gleichung (3) in Gleichung (4) ein, erhält man die Lösung des Aufgabenteils b)
c) Energie
Um die gesamte im Kondensator gespeicherte Energie zu erhalten, muss die Energiedichte über das von der elektrischen Energie gefüllte Gebiet zwischen den beiden Elektroden integriert werden.
Da die Energiedichte nur vom Radius
Alternativer Weg:
Zu diesem Ergebnis hätte man auch auf einem anderen Weg gelangen können. Für die in einer Kondensator gespeicherte Energie gilt auch
Die Kapazität
Setzt man jetzt Gleichung (7) in Gleichung (6) ein, erhält man
Lösung:
a)
b)
c)