Aufgabenstellung:
Zeigen Sie für den Reihenresonanzkreis, dass folgende Beziehungen gelten:
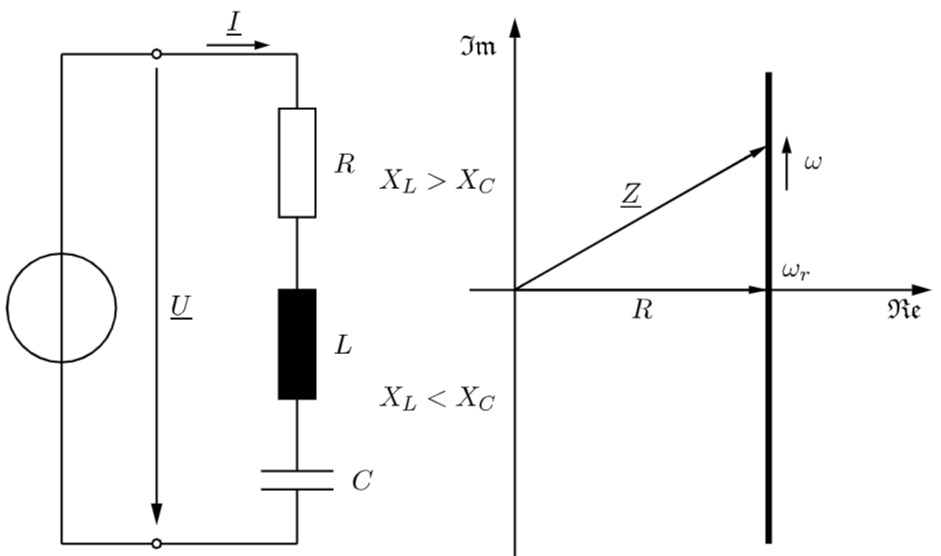
a) Im Resonanzfall
b) Bei Grenzfrequenzen
c) Leiten Sie aus dem Ansatz
d) Gehen Sie von den Definitionsgleichungen für Bandbreite
Lösungsweg:
a) Resonanzfall
Resonanzfall:
also folgt:
b) Grenzfrequenzen
Bandgrenzen
c) Beziehung Grenzfrequenz
Auszuwerten ist z. B. nur die Gleichung
da die zweite Beziehung mit negativer Klammer die gleichen Ergebnisse liefert:
Mit
Da der Wurzelausdruck für reale Bauelemente immer Werte liefert, die größer als der Wert
d) Herleitung Schwingkreisformel
Die Bandbreite ist definiert als die Differenz der beiden Grenzfrequenzen:
Durch einsetzen der unter c) hergeleiten Beziehung ergibt sich:
Die Güte ist definiert aus der Resonanzfrequenz bezogen auf die Bandbreite:
Einsetzen der Bandbreiteformel für
Häufig wird anstelle des Gütefaktors
Lösung:
siehe Lösungsweg