Aufgabenstellung:
In der Schaltung nach Bild a soll der Kondensator mit der Kapazität
a) Welchen Wert muss der Widerstand
b) Es ist der zeitliche Verlauf der Kondensatorspannung
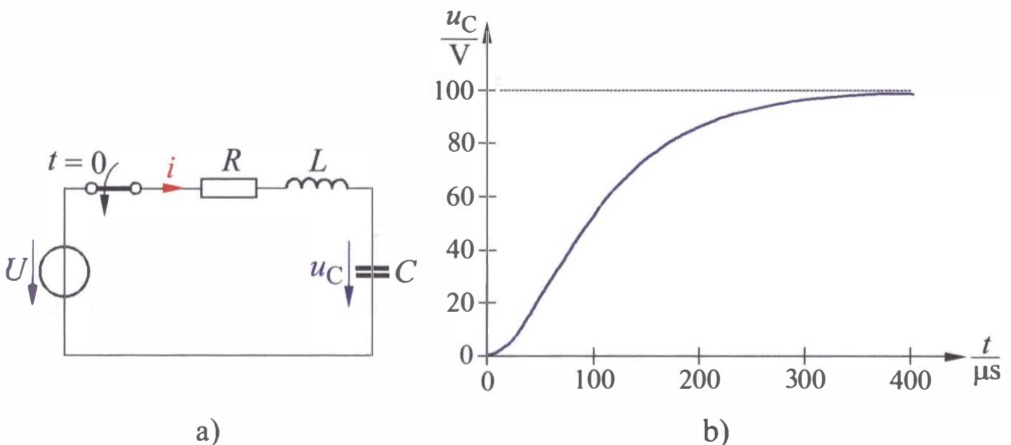
Bild Aufladen eines Kondensators nach dem aperiodischen Grenzfall. a) Gegebene Schaltung,
b) zeitlicher Verlauf der Kondensatorspannung
Lösungsweg:
a) Es lautet die Differenzialgleichung zur Bestimmung von
Zu deren Lösung wählen wir den Ansatz
Hierbei ist aus Bild a ersichtlich, dass die stationäre Kondensatorspannung
beträgt. Für die freie Kondensatorspannung
Hierbei lassen sich die Konstanten
Beim aperiodischen Grenzfall muss
sein. Hieraus erhalten wir den gesuchten Widerstand als
b) Wir erhalten die Doppelwurzel:
Beim vorliegenden aperiodischen Grenzfall lässt sich die angegebene Beziehung für
wobei
beträgt. Setzen wir die Ergebnisse ein, so erhalten wir die allgemeine Lösung für die gesuchte Kondensatorspannung als
Die hierin enthaltenen Konstanten
- ebenfalls
Hieraus folgt
Weiterhin muss im Zeitpunkt
Durch Einsetzen der Werte
Hieraus folgt
Setzen wir die gefundenen Werte ein, so erhalten wir die endgültige Lösung für die gesuchte Kondensatorspannung als
In Bild b ist dieser zeitliche Verlauf grafisch dargestellt.