Gleichspannung 

Wechselspannung

Unterschied In/Homogen

Basis, Basiswechsel

Abbildungsmatrizen

Funktionen bestimmen

Geraden und Ebenen

Gruppen

lineare abbildung 

quadratische ergänzung

Baustatik 1

Anfangswertprobleme :)

Differentialgleichungen

basis 

QR-Algorithmus

QR-Zerlegung

Cholesky-Zerlegung

Bild & Urbild

Zweigstromanalyse

Transistor als Thermometer

Investment

Teilfolgen

Epsilon Delta Kriterium

prinzip der virtuellen verrückung 

Linear Kombination

Folgen, Reihen und Potenzreihen

Flächenpressung

Arbeit 

Cholesky Zerlegung

Polynomfunktionen beschreiben

Zu Maß-und Integrationstheorie: Majorisierte Konvergenz

Teilchenphysik und Festkörperphysik

Orthogonaltrajektorien

test

Taylorreihen

Regel von de L'Hopital

Mathe

KRAFT

Grenzwert Funktion 

Folgenkriterium

ϵ-δ Kriterium 

Beweis Stetigkeit 

Wahrheitstabelle

2x2 Matrix

Matrix invertieren

Basiswechselsatz

Lineare Abbildunge 

Vorderrad fahradgabel lagerkräfte berechnen 

Spannungsregelung

Jordan Normal Form

Test

Induktion 

Jordan-Normalform

Ansatz der Störfunktion zur Bestimmung der Partikulären Lösung

Kurvenintegral

dlg mithilfe inhomogenen linearen system lösen

Inverse einer Matrix

Gleichmäßige Stetigkeit

addition

Regel von L´Hospital

Lineare Abbildungen

dimension eines Untervektorraumes bestimmen

Stationäre Stoffübertragung

Polplan, Prinzip der virtuellen Verrückungen

komplexe Ungleichungen 

Bidualräume

Dualräume

Taylorpolynome

Kern und Basis

Diagonalisieren einer Matrix

Rekursive Folgen

Exponentialreihe

Darstellungsmatrizen

restglied

Basiswechsel

Gamma Funktion

Newton Verfahren

Randwertaufgabe

Numerische Integration: Trapez- und Simpsonregel

Funktionenfolgen

dualräume

Dualraum

Komplexe Nullstellen

Chemie

Natascha Kirchmann

Differentialquotient

Folgedefinition des Funktionslimes

Grenzwerte und Stetigkeit 

Komplexe Zahlen

Kern und Bild 

Direkte Summe 

Koordinaten 

Exponentielle Verzinsung

Lineare Verzinsung

Festverzinsliche Wertpapiere

Stefan Schenke

<ol style="list-style-type: lower-alpha;">
<li>\[<br />\begin{aligned}<br />i(t=\infty) &amp;=0 \\<br />u_{C}(t=\infty) &amp;=0<br />\end{aligned}<br />\]</li>
<li>\[<br />\begin{aligned}<br />I(s) &amp;=i(t=0) \frac{s}{s^{2}+\frac{R}{L} s+\frac{1}{C L}}<br />\end{aligned}<br />\]</li>
<li>
<p>\[<br />\delta=\frac{R}{2 L}, \omega_{0}=\frac{1}{\sqrt{L C}}, s_{1,2}=-\delta \pm \sqrt{\delta^{2}-\omega_{0}^{2}}<br />\]</p>
</li>
<li>\[<br />\begin{aligned}<br />u_{R} &amp;=-R \cdot i_{L}=U \cdot \frac{R}{R_{\mathrm{i}}} \cdot\left(1-\frac{R}{2 \cdot L} \cdot t\right) \cdot \mathrm{e}^{-\frac{R}{2 \cdot L} \cdot t}<br />\end{aligned}<br />\]</li>
</ol>

<p>a) Spannung \( u_{C} \) und den Strom \( i \) jeweils für \( t=0 \) und \( t \rightarrow \infty \):</p>


<p>a) Spannung <mjx-container class="MathJax" jax="SVG"><svg alt=" u_{C} " style="vertical-align: -0.375ex" xmlns="http://www.w3.org/2000/svg" width="2.623ex" height="1.375ex" role="img" focusable="false" viewBox="0 -442 1159.4 607.6" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-5350-TEX-I-1D462" d="M21 287Q21 295 30 318T55 370T99 420T158 442Q204 442 227 417T250 358Q250 340 216 246T182 105Q182 62 196 45T238 27T291 44T328 78L339 95Q341 99 377 247Q407 367 413 387T427 416Q444 431 463 431Q480 431 488 421T496 402L420 84Q419 79 419 68Q419 43 426 35T447 26Q469 29 482 57T512 145Q514 153 532 153Q551 153 551 144Q550 139 549 130T540 98T523 55T498 17T462 -8Q454 -10 438 -10Q372 -10 347 46Q345 45 336 36T318 21T296 6T267 -6T233 -11Q189 -11 155 7Q103 38 103 113Q103 170 138 262T173 379Q173 380 173 381Q173 390 173 393T169 400T158 404H154Q131 404 112 385T82 344T65 302T57 280Q55 278 41 278H27Q21 284 21 287Z"></path><path id="MJX-5350-TEX-I-1D436" d="M50 252Q50 367 117 473T286 641T490 704Q580 704 633 653Q642 643 648 636T656 626L657 623Q660 623 684 649Q691 655 699 663T715 679T725 690L740 705H746Q760 705 760 698Q760 694 728 561Q692 422 692 421Q690 416 687 415T669 413H653Q647 419 647 422Q647 423 648 429T650 449T651 481Q651 552 619 605T510 659Q484 659 454 652T382 628T299 572T226 479Q194 422 175 346T156 222Q156 108 232 58Q280 24 350 24Q441 24 512 92T606 240Q610 253 612 255T628 257Q648 257 648 248Q648 243 647 239Q618 132 523 55T319 -22Q206 -22 128 53T50 252Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"><g data-mml-node="math"><g data-mml-node="msub"><g data-mml-node="mi"><use xlink:href="#MJX-5350-TEX-I-1D462"></use></g><g data-mml-node="TeXAtom" transform="translate(572, -150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mi"><use xlink:href="#MJX-5350-TEX-I-1D436"></use></g></g></g></g></g></svg></mjx-container> und den Strom <mjx-container class="MathJax" jax="SVG"><svg alt=" i " style="vertical-align: -0.025ex" xmlns="http://www.w3.org/2000/svg" width="0.781ex" height="1.52ex" role="img" focusable="false" viewBox="0 -661 345 672" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-5351-TEX-I-1D456" d="M184 600Q184 624 203 642T247 661Q265 661 277 649T290 619Q290 596 270 577T226 557Q211 557 198 567T184 600ZM21 287Q21 295 30 318T54 369T98 420T158 442Q197 442 223 419T250 357Q250 340 236 301T196 196T154 83Q149 61 149 51Q149 26 166 26Q175 26 185 29T208 43T235 78T260 137Q263 149 265 151T282 153Q302 153 302 143Q302 135 293 112T268 61T223 11T161 -11Q129 -11 102 10T74 74Q74 91 79 106T122 220Q160 321 166 341T173 380Q173 404 156 404H154Q124 404 99 371T61 287Q60 286 59 284T58 281T56 279T53 278T49 278T41 278H27Q21 284 21 287Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"><g data-mml-node="math"><g data-mml-node="mi"><use xlink:href="#MJX-5351-TEX-I-1D456"></use></g></g></g></svg></mjx-container> jeweils für <mjx-container class="MathJax" jax="SVG"><svg alt=" t=0 " style="vertical-align: -0.186ex" xmlns="http://www.w3.org/2000/svg" width="4.965ex" height="1.692ex" role="img" focusable="false" viewBox="0 -666 2194.6 748" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-5352-TEX-I-1D461" d="M26 385Q19 392 19 395Q19 399 22 411T27 425Q29 430 36 430T87 431H140L159 511Q162 522 166 540T173 566T179 586T187 603T197 615T211 624T229 626Q247 625 254 615T261 596Q261 589 252 549T232 470L222 433Q222 431 272 431H323Q330 424 330 420Q330 398 317 385H210L174 240Q135 80 135 68Q135 26 162 26Q197 26 230 60T283 144Q285 150 288 151T303 153H307Q322 153 322 145Q322 142 319 133Q314 117 301 95T267 48T216 6T155 -11Q125 -11 98 4T59 56Q57 64 57 83V101L92 241Q127 382 128 383Q128 385 77 385H26Z"></path><path id="MJX-5352-TEX-N-3D" d="M56 347Q56 360 70 367H707Q722 359 722 347Q722 336 708 328L390 327H72Q56 332 56 347ZM56 153Q56 168 72 173H708Q722 163 722 153Q722 140 707 133H70Q56 140 56 153Z"></path><path id="MJX-5352-TEX-N-30" d="M96 585Q152 666 249 666Q297 666 345 640T423 548Q460 465 460 320Q460 165 417 83Q397 41 362 16T301 -15T250 -22Q224 -22 198 -16T137 16T82 83Q39 165 39 320Q39 494 96 585ZM321 597Q291 629 250 629Q208 629 178 597Q153 571 145 525T137 333Q137 175 145 125T181 46Q209 16 250 16Q290 16 318 46Q347 76 354 130T362 333Q362 478 354 524T321 597Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"><g data-mml-node="math"><g data-mml-node="mi"><use xlink:href="#MJX-5352-TEX-I-1D461"></use></g><g data-mml-node="mo" transform="translate(638.8, 0)"><use xlink:href="#MJX-5352-TEX-N-3D"></use></g><g data-mml-node="mn" transform="translate(1694.6, 0)"><use xlink:href="#MJX-5352-TEX-N-30"></use></g></g></g></svg></mjx-container> und <mjx-container class="MathJax" jax="SVG"><svg alt=" t \rightarrow \infty " style="vertical-align: -0.025ex" xmlns="http://www.w3.org/2000/svg" width="6.599ex" height="1.441ex" role="img" focusable="false" viewBox="0 -626 2916.6 637" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-5353-TEX-I-1D461" d="M26 385Q19 392 19 395Q19 399 22 411T27 425Q29 430 36 430T87 431H140L159 511Q162 522 166 540T173 566T179 586T187 603T197 615T211 624T229 626Q247 625 254 615T261 596Q261 589 252 549T232 470L222 433Q222 431 272 431H323Q330 424 330 420Q330 398 317 385H210L174 240Q135 80 135 68Q135 26 162 26Q197 26 230 60T283 144Q285 150 288 151T303 153H307Q322 153 322 145Q322 142 319 133Q314 117 301 95T267 48T216 6T155 -11Q125 -11 98 4T59 56Q57 64 57 83V101L92 241Q127 382 128 383Q128 385 77 385H26Z"></path><path id="MJX-5353-TEX-N-2192" d="M56 237T56 250T70 270H835Q719 357 692 493Q692 494 692 496T691 499Q691 511 708 511H711Q720 511 723 510T729 506T732 497T735 481T743 456Q765 389 816 336T935 261Q944 258 944 250Q944 244 939 241T915 231T877 212Q836 186 806 152T761 85T740 35T732 4Q730 -6 727 -8T711 -11Q691 -11 691 0Q691 7 696 25Q728 151 835 230H70Q56 237 56 250Z"></path><path id="MJX-5353-TEX-N-221E" d="M55 217Q55 305 111 373T254 442Q342 442 419 381Q457 350 493 303L507 284L514 294Q618 442 747 442Q833 442 888 374T944 214Q944 128 889 59T743 -11Q657 -11 580 50Q542 81 506 128L492 147L485 137Q381 -11 252 -11Q166 -11 111 57T55 217ZM907 217Q907 285 869 341T761 397Q740 397 720 392T682 378T648 359T619 335T594 310T574 285T559 263T548 246L543 238L574 198Q605 158 622 138T664 94T714 61T765 51Q827 51 867 100T907 217ZM92 214Q92 145 131 89T239 33Q357 33 456 193L425 233Q364 312 334 337Q285 380 233 380Q171 380 132 331T92 214Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"><g data-mml-node="math"><g data-mml-node="mi"><use xlink:href="#MJX-5353-TEX-I-1D461"></use></g><g data-mml-node="mo" transform="translate(638.8, 0)"><use xlink:href="#MJX-5353-TEX-N-2192"></use></g><g data-mml-node="mi" transform="translate(1916.6, 0)"><use xlink:href="#MJX-5353-TEX-N-221E"></use></g></g></g></svg></mjx-container>:</p>


<p>Im statischen Zustand für \( t &lt; 0 \) verhalten sich die Induktivität wie ein Kurzschluss und die Kapazität wie ein Leerlauf. Außerdem können sich an der Induktivität der Strom und an der Kapazität die Spannung nicht sprunghaft ändern.</p>


<p>Im statischen Zustand für <mjx-container class="MathJax" jax="SVG"><svg alt=" t < 0 " style="vertical-align: -0.09ex" xmlns="http://www.w3.org/2000/svg" width="4.965ex" height="1.597ex" role="img" focusable="false" viewBox="0 -666 2194.6 706" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-5354-TEX-I-1D461" d="M26 385Q19 392 19 395Q19 399 22 411T27 425Q29 430 36 430T87 431H140L159 511Q162 522 166 540T173 566T179 586T187 603T197 615T211 624T229 626Q247 625 254 615T261 596Q261 589 252 549T232 470L222 433Q222 431 272 431H323Q330 424 330 420Q330 398 317 385H210L174 240Q135 80 135 68Q135 26 162 26Q197 26 230 60T283 144Q285 150 288 151T303 153H307Q322 153 322 145Q322 142 319 133Q314 117 301 95T267 48T216 6T155 -11Q125 -11 98 4T59 56Q57 64 57 83V101L92 241Q127 382 128 383Q128 385 77 385H26Z"></path><path id="MJX-5354-TEX-N-3C" d="M694 -11T694 -19T688 -33T678 -40Q671 -40 524 29T234 166L90 235Q83 240 83 250Q83 261 91 266Q664 540 678 540Q681 540 687 534T694 519T687 505Q686 504 417 376L151 250L417 124Q686 -4 687 -5Q694 -11 694 -19Z"></path><path id="MJX-5354-TEX-N-30" d="M96 585Q152 666 249 666Q297 666 345 640T423 548Q460 465 460 320Q460 165 417 83Q397 41 362 16T301 -15T250 -22Q224 -22 198 -16T137 16T82 83Q39 165 39 320Q39 494 96 585ZM321 597Q291 629 250 629Q208 629 178 597Q153 571 145 525T137 333Q137 175 145 125T181 46Q209 16 250 16Q290 16 318 46Q347 76 354 130T362 333Q362 478 354 524T321 597Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"><g data-mml-node="math"><g data-mml-node="mi"><use xlink:href="#MJX-5354-TEX-I-1D461"></use></g><g data-mml-node="mo" transform="translate(638.8, 0)"><use xlink:href="#MJX-5354-TEX-N-3C"></use></g><g data-mml-node="mn" transform="translate(1694.6, 0)"><use xlink:href="#MJX-5354-TEX-N-30"></use></g></g></g></svg></mjx-container> verhalten sich die Induktivität wie ein Kurzschluss und die Kapazität wie ein Leerlauf. Außerdem können sich an der Induktivität der Strom und an der Kapazität die Spannung nicht sprunghaft ändern.</p>


<p>\[<br />\begin{aligned}<br />i(t=0) &amp;=\frac{U}{R_{\mathrm{i}}} \\<br />u_{C}(t=0) &amp;=0<br />\end{aligned}<br />\]</p>


<p>\[<br />\begin{aligned}<br />i(t=\infty) &amp;=0 \\<br />u_{C}(t=\infty) &amp;=0<br />\end{aligned}<br />\]</p>


<p>b) Bestimmung der Laplacetransformierte \( I(s) \) des Stromes \( i(t) \)</p>


<p>b) Bestimmung der Laplacetransformierte <mjx-container class="MathJax" jax="SVG"><svg alt=" I(s) " style="vertical-align: -0.566ex" xmlns="http://www.w3.org/2000/svg" width="3.962ex" height="2.262ex" role="img" focusable="false" viewBox="0 -750 1751 1000" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-5357-TEX-I-1D43C" d="M43 1Q26 1 26 10Q26 12 29 24Q34 43 39 45Q42 46 54 46H60Q120 46 136 53Q137 53 138 54Q143 56 149 77T198 273Q210 318 216 344Q286 624 286 626Q284 630 284 631Q274 637 213 637H193Q184 643 189 662Q193 677 195 680T209 683H213Q285 681 359 681Q481 681 487 683H497Q504 676 504 672T501 655T494 639Q491 637 471 637Q440 637 407 634Q393 631 388 623Q381 609 337 432Q326 385 315 341Q245 65 245 59Q245 52 255 50T307 46H339Q345 38 345 37T342 19Q338 6 332 0H316Q279 2 179 2Q143 2 113 2T65 2T43 1Z"></path><path id="MJX-5357-TEX-N-28" d="M94 250Q94 319 104 381T127 488T164 576T202 643T244 695T277 729T302 750H315H319Q333 750 333 741Q333 738 316 720T275 667T226 581T184 443T167 250T184 58T225 -81T274 -167T316 -220T333 -241Q333 -250 318 -250H315H302L274 -226Q180 -141 137 -14T94 250Z"></path><path id="MJX-5357-TEX-I-1D460" d="M131 289Q131 321 147 354T203 415T300 442Q362 442 390 415T419 355Q419 323 402 308T364 292Q351 292 340 300T328 326Q328 342 337 354T354 372T367 378Q368 378 368 379Q368 382 361 388T336 399T297 405Q249 405 227 379T204 326Q204 301 223 291T278 274T330 259Q396 230 396 163Q396 135 385 107T352 51T289 7T195 -10Q118 -10 86 19T53 87Q53 126 74 143T118 160Q133 160 146 151T160 120Q160 94 142 76T111 58Q109 57 108 57T107 55Q108 52 115 47T146 34T201 27Q237 27 263 38T301 66T318 97T323 122Q323 150 302 164T254 181T195 196T148 231Q131 256 131 289Z"></path><path id="MJX-5357-TEX-N-29" d="M60 749L64 750Q69 750 74 750H86L114 726Q208 641 251 514T294 250Q294 182 284 119T261 12T224 -76T186 -143T145 -194T113 -227T90 -246Q87 -249 86 -250H74Q66 -250 63 -250T58 -247T55 -238Q56 -237 66 -225Q221 -64 221 250T66 725Q56 737 55 738Q55 746 60 749Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"><g data-mml-node="math"><g data-mml-node="mi"><use xlink:href="#MJX-5357-TEX-I-1D43C"></use></g><g data-mml-node="mo" transform="translate(504, 0)"><use xlink:href="#MJX-5357-TEX-N-28"></use></g><g data-mml-node="mi" transform="translate(893, 0)"><use xlink:href="#MJX-5357-TEX-I-1D460"></use></g><g data-mml-node="mo" transform="translate(1362, 0)"><use xlink:href="#MJX-5357-TEX-N-29"></use></g></g></g></svg></mjx-container> des Stromes <mjx-container class="MathJax" jax="SVG"><svg alt=" i(t) " style="vertical-align: -0.566ex" xmlns="http://www.w3.org/2000/svg" width="3.357ex" height="2.262ex" role="img" focusable="false" viewBox="0 -750 1484 1000" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-5358-TEX-I-1D456" d="M184 600Q184 624 203 642T247 661Q265 661 277 649T290 619Q290 596 270 577T226 557Q211 557 198 567T184 600ZM21 287Q21 295 30 318T54 369T98 420T158 442Q197 442 223 419T250 357Q250 340 236 301T196 196T154 83Q149 61 149 51Q149 26 166 26Q175 26 185 29T208 43T235 78T260 137Q263 149 265 151T282 153Q302 153 302 143Q302 135 293 112T268 61T223 11T161 -11Q129 -11 102 10T74 74Q74 91 79 106T122 220Q160 321 166 341T173 380Q173 404 156 404H154Q124 404 99 371T61 287Q60 286 59 284T58 281T56 279T53 278T49 278T41 278H27Q21 284 21 287Z"></path><path id="MJX-5358-TEX-N-28" d="M94 250Q94 319 104 381T127 488T164 576T202 643T244 695T277 729T302 750H315H319Q333 750 333 741Q333 738 316 720T275 667T226 581T184 443T167 250T184 58T225 -81T274 -167T316 -220T333 -241Q333 -250 318 -250H315H302L274 -226Q180 -141 137 -14T94 250Z"></path><path id="MJX-5358-TEX-I-1D461" d="M26 385Q19 392 19 395Q19 399 22 411T27 425Q29 430 36 430T87 431H140L159 511Q162 522 166 540T173 566T179 586T187 603T197 615T211 624T229 626Q247 625 254 615T261 596Q261 589 252 549T232 470L222 433Q222 431 272 431H323Q330 424 330 420Q330 398 317 385H210L174 240Q135 80 135 68Q135 26 162 26Q197 26 230 60T283 144Q285 150 288 151T303 153H307Q322 153 322 145Q322 142 319 133Q314 117 301 95T267 48T216 6T155 -11Q125 -11 98 4T59 56Q57 64 57 83V101L92 241Q127 382 128 383Q128 385 77 385H26Z"></path><path id="MJX-5358-TEX-N-29" d="M60 749L64 750Q69 750 74 750H86L114 726Q208 641 251 514T294 250Q294 182 284 119T261 12T224 -76T186 -143T145 -194T113 -227T90 -246Q87 -249 86 -250H74Q66 -250 63 -250T58 -247T55 -238Q56 -237 66 -225Q221 -64 221 250T66 725Q56 737 55 738Q55 746 60 749Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"><g data-mml-node="math"><g data-mml-node="mi"><use xlink:href="#MJX-5358-TEX-I-1D456"></use></g><g data-mml-node="mo" transform="translate(345, 0)"><use xlink:href="#MJX-5358-TEX-N-28"></use></g><g data-mml-node="mi" transform="translate(734, 0)"><use xlink:href="#MJX-5358-TEX-I-1D461"></use></g><g data-mml-node="mo" transform="translate(1095, 0)"><use xlink:href="#MJX-5358-TEX-N-29"></use></g></g></g></svg></mjx-container></p>


<p>\( I(s) \) lässt sich über den Stromteiler berechnen:</p>


<p><mjx-container class="MathJax" jax="SVG"><svg alt=" I(s) " style="vertical-align: -0.566ex" xmlns="http://www.w3.org/2000/svg" width="3.962ex" height="2.262ex" role="img" focusable="false" viewBox="0 -750 1751 1000" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-5359-TEX-I-1D43C" d="M43 1Q26 1 26 10Q26 12 29 24Q34 43 39 45Q42 46 54 46H60Q120 46 136 53Q137 53 138 54Q143 56 149 77T198 273Q210 318 216 344Q286 624 286 626Q284 630 284 631Q274 637 213 637H193Q184 643 189 662Q193 677 195 680T209 683H213Q285 681 359 681Q481 681 487 683H497Q504 676 504 672T501 655T494 639Q491 637 471 637Q440 637 407 634Q393 631 388 623Q381 609 337 432Q326 385 315 341Q245 65 245 59Q245 52 255 50T307 46H339Q345 38 345 37T342 19Q338 6 332 0H316Q279 2 179 2Q143 2 113 2T65 2T43 1Z"></path><path id="MJX-5359-TEX-N-28" d="M94 250Q94 319 104 381T127 488T164 576T202 643T244 695T277 729T302 750H315H319Q333 750 333 741Q333 738 316 720T275 667T226 581T184 443T167 250T184 58T225 -81T274 -167T316 -220T333 -241Q333 -250 318 -250H315H302L274 -226Q180 -141 137 -14T94 250Z"></path><path id="MJX-5359-TEX-I-1D460" d="M131 289Q131 321 147 354T203 415T300 442Q362 442 390 415T419 355Q419 323 402 308T364 292Q351 292 340 300T328 326Q328 342 337 354T354 372T367 378Q368 378 368 379Q368 382 361 388T336 399T297 405Q249 405 227 379T204 326Q204 301 223 291T278 274T330 259Q396 230 396 163Q396 135 385 107T352 51T289 7T195 -10Q118 -10 86 19T53 87Q53 126 74 143T118 160Q133 160 146 151T160 120Q160 94 142 76T111 58Q109 57 108 57T107 55Q108 52 115 47T146 34T201 27Q237 27 263 38T301 66T318 97T323 122Q323 150 302 164T254 181T195 196T148 231Q131 256 131 289Z"></path><path id="MJX-5359-TEX-N-29" d="M60 749L64 750Q69 750 74 750H86L114 726Q208 641 251 514T294 250Q294 182 284 119T261 12T224 -76T186 -143T145 -194T113 -227T90 -246Q87 -249 86 -250H74Q66 -250 63 -250T58 -247T55 -238Q56 -237 66 -225Q221 -64 221 250T66 725Q56 737 55 738Q55 746 60 749Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"><g data-mml-node="math"><g data-mml-node="mi"><use xlink:href="#MJX-5359-TEX-I-1D43C"></use></g><g data-mml-node="mo" transform="translate(504, 0)"><use xlink:href="#MJX-5359-TEX-N-28"></use></g><g data-mml-node="mi" transform="translate(893, 0)"><use xlink:href="#MJX-5359-TEX-I-1D460"></use></g><g data-mml-node="mo" transform="translate(1362, 0)"><use xlink:href="#MJX-5359-TEX-N-29"></use></g></g></g></svg></mjx-container> lässt sich über den Stromteiler berechnen:</p>


<p>\[<br />\begin{aligned}<br />I(s) &amp;=\frac{i(t=0)}{s} \frac{s L}{s L+R+\frac{1}{s C}} \\<br />&amp;=i(t=0) \frac{L}{s L+R+\frac{1}{s C}} \\<br />&amp;=i(t=0) \frac{1}{s+\frac{R}{L}+\frac{1}{s C L}} \\<br />&amp;=i(t=0) \frac{s}{s^{2}+\frac{R}{L} s+\frac{1}{C L}}<br />\end{aligned}<br />\]</p>


<p>c) Kriechfall und der aperiodische Grenzfall</p>


<p>\[<br />\begin{aligned}<br />I(s) &amp;=i(t=0) \cdot \frac{s}{s^{2}+\frac{R}{L} \cdot s+\frac{1}{C L}} \\<br />&amp;=i(t=0) \cdot \frac{s}{s^{2}+2 \cdot \delta \cdot s+\omega_{0}^{2}}, \text { bzw. mit } \omega_{0}^{2}=\omega^{2}+\delta^{2}: \\<br />=&amp;\left\{\begin{array}{ll}<br />i(t=0) \cdot \frac{s}{s^{2}+2 \cdot \delta \cdot s+\omega^{2}+\delta^{2}} &amp; \text { für } \omega_{0} &gt; \delta,(\text { Schwingfall }) \\<br />i(t=0) \cdot \frac{s}{(s+\delta)^{2}} &amp; \text { für } \omega_{0}=\delta,(\text { aper. Grenzfall }), \\<br />i(t=0) \cdot \frac{s}{(s+a)(s+b)} &amp; \text { für } \omega_{0} &lt; \delta,(\text { Kriechfall })<br />\end{array}\right.<br />\end{aligned}<br />\]</p>


<p>\[<br />\delta=\frac{R}{2 L}, \omega_{0}=\frac{1}{\sqrt{L C}}, s_{1,2}=-\delta \pm \sqrt{\delta^{2}-\omega_{0}^{2}}<br />\]</p>


<p>d) \( u_{R}(t) \) für den aperiodischen Grenzfall</p>


<p>d) <mjx-container class="MathJax" jax="SVG"><svg alt=" u_{R}(t) " style="vertical-align: -0.566ex" xmlns="http://www.w3.org/2000/svg" width="5.198ex" height="2.262ex" role="img" focusable="false" viewBox="0 -750 2297.7 1000" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-5364-TEX-I-1D462" d="M21 287Q21 295 30 318T55 370T99 420T158 442Q204 442 227 417T250 358Q250 340 216 246T182 105Q182 62 196 45T238 27T291 44T328 78L339 95Q341 99 377 247Q407 367 413 387T427 416Q444 431 463 431Q480 431 488 421T496 402L420 84Q419 79 419 68Q419 43 426 35T447 26Q469 29 482 57T512 145Q514 153 532 153Q551 153 551 144Q550 139 549 130T540 98T523 55T498 17T462 -8Q454 -10 438 -10Q372 -10 347 46Q345 45 336 36T318 21T296 6T267 -6T233 -11Q189 -11 155 7Q103 38 103 113Q103 170 138 262T173 379Q173 380 173 381Q173 390 173 393T169 400T158 404H154Q131 404 112 385T82 344T65 302T57 280Q55 278 41 278H27Q21 284 21 287Z"></path><path id="MJX-5364-TEX-I-1D445" d="M230 637Q203 637 198 638T193 649Q193 676 204 682Q206 683 378 683Q550 682 564 680Q620 672 658 652T712 606T733 563T739 529Q739 484 710 445T643 385T576 351T538 338L545 333Q612 295 612 223Q612 212 607 162T602 80V71Q602 53 603 43T614 25T640 16Q668 16 686 38T712 85Q717 99 720 102T735 105Q755 105 755 93Q755 75 731 36Q693 -21 641 -21H632Q571 -21 531 4T487 82Q487 109 502 166T517 239Q517 290 474 313Q459 320 449 321T378 323H309L277 193Q244 61 244 59Q244 55 245 54T252 50T269 48T302 46H333Q339 38 339 37T336 19Q332 6 326 0H311Q275 2 180 2Q146 2 117 2T71 2T50 1Q33 1 33 10Q33 12 36 24Q41 43 46 45Q50 46 61 46H67Q94 46 127 49Q141 52 146 61Q149 65 218 339T287 628Q287 635 230 637ZM630 554Q630 586 609 608T523 636Q521 636 500 636T462 637H440Q393 637 386 627Q385 624 352 494T319 361Q319 360 388 360Q466 361 492 367Q556 377 592 426Q608 449 619 486T630 554Z"></path><path id="MJX-5364-TEX-N-28" d="M94 250Q94 319 104 381T127 488T164 576T202 643T244 695T277 729T302 750H315H319Q333 750 333 741Q333 738 316 720T275 667T226 581T184 443T167 250T184 58T225 -81T274 -167T316 -220T333 -241Q333 -250 318 -250H315H302L274 -226Q180 -141 137 -14T94 250Z"></path><path id="MJX-5364-TEX-I-1D461" d="M26 385Q19 392 19 395Q19 399 22 411T27 425Q29 430 36 430T87 431H140L159 511Q162 522 166 540T173 566T179 586T187 603T197 615T211 624T229 626Q247 625 254 615T261 596Q261 589 252 549T232 470L222 433Q222 431 272 431H323Q330 424 330 420Q330 398 317 385H210L174 240Q135 80 135 68Q135 26 162 26Q197 26 230 60T283 144Q285 150 288 151T303 153H307Q322 153 322 145Q322 142 319 133Q314 117 301 95T267 48T216 6T155 -11Q125 -11 98 4T59 56Q57 64 57 83V101L92 241Q127 382 128 383Q128 385 77 385H26Z"></path><path id="MJX-5364-TEX-N-29" d="M60 749L64 750Q69 750 74 750H86L114 726Q208 641 251 514T294 250Q294 182 284 119T261 12T224 -76T186 -143T145 -194T113 -227T90 -246Q87 -249 86 -250H74Q66 -250 63 -250T58 -247T55 -238Q56 -237 66 -225Q221 -64 221 250T66 725Q56 737 55 738Q55 746 60 749Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"><g data-mml-node="math"><g data-mml-node="msub"><g data-mml-node="mi"><use xlink:href="#MJX-5364-TEX-I-1D462"></use></g><g data-mml-node="TeXAtom" transform="translate(572, -150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mi"><use xlink:href="#MJX-5364-TEX-I-1D445"></use></g></g></g><g data-mml-node="mo" transform="translate(1158.7, 0)"><use xlink:href="#MJX-5364-TEX-N-28"></use></g><g data-mml-node="mi" transform="translate(1547.7, 0)"><use xlink:href="#MJX-5364-TEX-I-1D461"></use></g><g data-mml-node="mo" transform="translate(1908.7, 0)"><use xlink:href="#MJX-5364-TEX-N-29"></use></g></g></g></svg></mjx-container> für den aperiodischen Grenzfall</p>


<p>aperiodischer Grenzfall \( \omega_{0}=\delta \) :</p>


<p>aperiodischer Grenzfall <mjx-container class="MathJax" jax="SVG"><svg alt=" \omega_{0}=\delta " style="vertical-align: -0.375ex" xmlns="http://www.w3.org/2000/svg" width="6.342ex" height="1.997ex" role="img" focusable="false" viewBox="0 -717 2803.1 882.6" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-5365-TEX-I-1D714" d="M495 384Q495 406 514 424T555 443Q574 443 589 425T604 364Q604 334 592 278T555 155T483 38T377 -11Q297 -11 267 66Q266 68 260 61Q201 -11 125 -11Q15 -11 15 139Q15 230 56 325T123 434Q135 441 147 436Q160 429 160 418Q160 406 140 379T94 306T62 208Q61 202 61 187Q61 124 85 100T143 76Q201 76 245 129L253 137V156Q258 297 317 297Q348 297 348 261Q348 243 338 213T318 158L308 135Q309 133 310 129T318 115T334 97T358 83T393 76Q456 76 501 148T546 274Q546 305 533 325T508 357T495 384Z"></path><path id="MJX-5365-TEX-N-30" d="M96 585Q152 666 249 666Q297 666 345 640T423 548Q460 465 460 320Q460 165 417 83Q397 41 362 16T301 -15T250 -22Q224 -22 198 -16T137 16T82 83Q39 165 39 320Q39 494 96 585ZM321 597Q291 629 250 629Q208 629 178 597Q153 571 145 525T137 333Q137 175 145 125T181 46Q209 16 250 16Q290 16 318 46Q347 76 354 130T362 333Q362 478 354 524T321 597Z"></path><path id="MJX-5365-TEX-N-3D" d="M56 347Q56 360 70 367H707Q722 359 722 347Q722 336 708 328L390 327H72Q56 332 56 347ZM56 153Q56 168 72 173H708Q722 163 722 153Q722 140 707 133H70Q56 140 56 153Z"></path><path id="MJX-5365-TEX-I-1D6FF" d="M195 609Q195 656 227 686T302 717Q319 716 351 709T407 697T433 690Q451 682 451 662Q451 644 438 628T403 612Q382 612 348 641T288 671T249 657T235 628Q235 584 334 463Q401 379 401 292Q401 169 340 80T205 -10H198Q127 -10 83 36T36 153Q36 286 151 382Q191 413 252 434Q252 435 245 449T230 481T214 521T201 566T195 609ZM112 130Q112 83 136 55T204 27Q233 27 256 51T291 111T309 178T316 232Q316 267 309 298T295 344T269 400L259 396Q215 381 183 342T137 256T118 179T112 130Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"><g data-mml-node="math"><g data-mml-node="msub"><g data-mml-node="mi"><use xlink:href="#MJX-5365-TEX-I-1D714"></use></g><g data-mml-node="TeXAtom" transform="translate(622, -150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mn"><use xlink:href="#MJX-5365-TEX-N-30"></use></g></g></g><g data-mml-node="mo" transform="translate(1303.3, 0)"><use xlink:href="#MJX-5365-TEX-N-3D"></use></g><g data-mml-node="mi" transform="translate(2359.1, 0)"><use xlink:href="#MJX-5365-TEX-I-1D6FF"></use></g></g></g></svg></mjx-container> :</p>


<p>\[<br />\begin{aligned}<br />I(s) &amp;=I_{0} \cdot \frac{s}{(s+\delta)^{2}} \quad \text { mit } \quad \delta=\frac{R}{2 \cdot L} \\<br />i &amp;=i(t=0) \cdot\left(1-\frac{R}{2 \cdot L} \cdot t\right) \cdot \mathrm{e}^{-\frac{R}{2 \cdot L} \cdot t} \\<br />&amp;=\frac{U}{R_{\mathrm{i}}} \cdot\left(1-\frac{R}{2 \cdot L} \cdot t\right) \cdot \mathrm{e}^{-\frac{R}{2 \cdot L} \cdot t} \\<br />u_{R} &amp;=-R \cdot i_{L}=U \cdot \frac{R}{R_{\mathrm{i}}} \cdot\left(1-\frac{R}{2 \cdot L} \cdot t\right) \cdot \mathrm{e}^{-\frac{R}{2 \cdot L} \cdot t}<br />\end{aligned}<br />\]</p>

<p>Für \( t &lt; 0 \) sind alle Ströme und Spannungen in dem skizzierten Netzwerk zeitlich konstant. Zum Zeitpunkt \( t=0 \) wird der Schalter \( S \) geöffnet.</p>
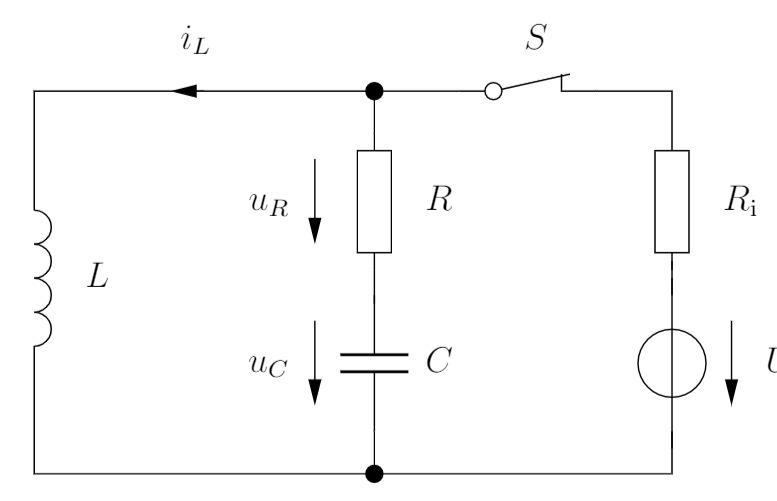
<p><img src="https://storage.googleapis.com/max-academy-image-bucket/6072cb91b1cc102914f9ab0c.png" alt="Abbildung" /></p>
<ol style="list-style-type: lower-alpha;">
<li>Bestimmen Sie die Spannung \( u_{C} \) und den Strom \( i \) jeweils für \( t=0 \) und \( t \rightarrow \infty \).</li>
<li>Bestimmen Sie die Laplacetransformierte \( I(s) \) des Stromes \( i(t) \)</li>
<li>Bestimmen Sie anhand \( I(s) \), für welche Werte der Bauelemente der Schwingfall, der Kriechfall und der aperiodische Grenzfall auftreten.</li>
<li>Berechnen Sie \( u_{R}(t) \) für den aperiodischen Grenzfall.</li>
</ol>

Dies ist eine interaktive Aufgabe zu: Gleichspannung  mit praktischen Tipps zum Lösen und einer Zusammenfassung der nötigen Theorie

Aufgabenstellung:

Lösungsweg:

Lösung: