Aufgabenstellung:
Gegeben ist untenstehende Schaltung mit den Werten:
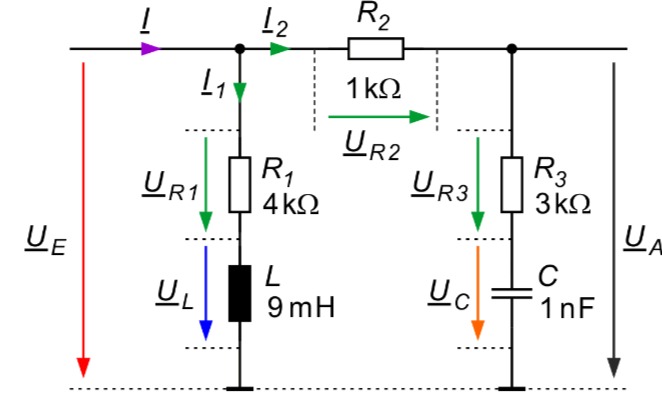
a) Es ist das vollständige Zeigerdiagramm aller Ströme und Spannungen bei der Frequenz zu zeichnen, bei der
b) Welches Spannungsteilerverhältnis
c) Mit welcher Impedanz
Lösungsweg:
a) Zeigerdiagramm
Beide betragsmäßig gleich bedeutet:
Hieraus erhält man die Gleichung, aus der sich die Frequenz bestimmen lässt:
Einsetzen der Zahlenwerte ergibt:
Mit dieser Frequenz erhält man die beiden Scheinwiderstände
Gegeben:
Annahme:
d.h.
Mit der vorgegebenen Länge von
Die Zeigerlängen von
Die Ausgangsspannung
Man liest im Zeigerdiagramm die Länge ab:
(auch Satz des Pythagoras möglich:
Konstruktion
Zur Konstruktion der Spannungen und Ströme in
Da durch
Die vektorielle Summe ist
Daher Thaleskreis über
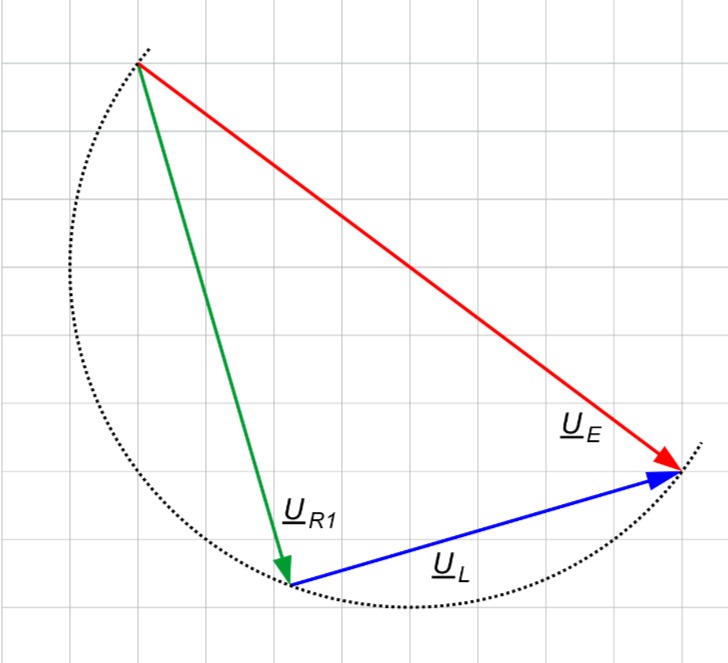
Für die Spannungen
(Pythagoras)
Nach dem Strom
Einsetzen der Zahlenwerte ergibt:
Die Spannung über
Mit dem Längenmaßstab ergibt sich
Konstruktion
Vom Koordinatennullpunkt wird also ein Kreisbogen mit der Länge
Wo dieser Bogen den Thaleskreis schneidet, ist der Zielpunkt von
In der gleichen Richtung, in der die Spannung
Die Spannung
Man liest ab
Der Eingangsstrom
Es zeigt sich, dass die Richtung des Stromes
Man liest die Länge ab:
Länge
b) Spannungsverhältnis und Phasenlage
Vorher ermittelt:
Phasenlage (siehe Zeigerdiagramm):
c) Impedanz
Da
Vollständiges Zeigerdiagramm
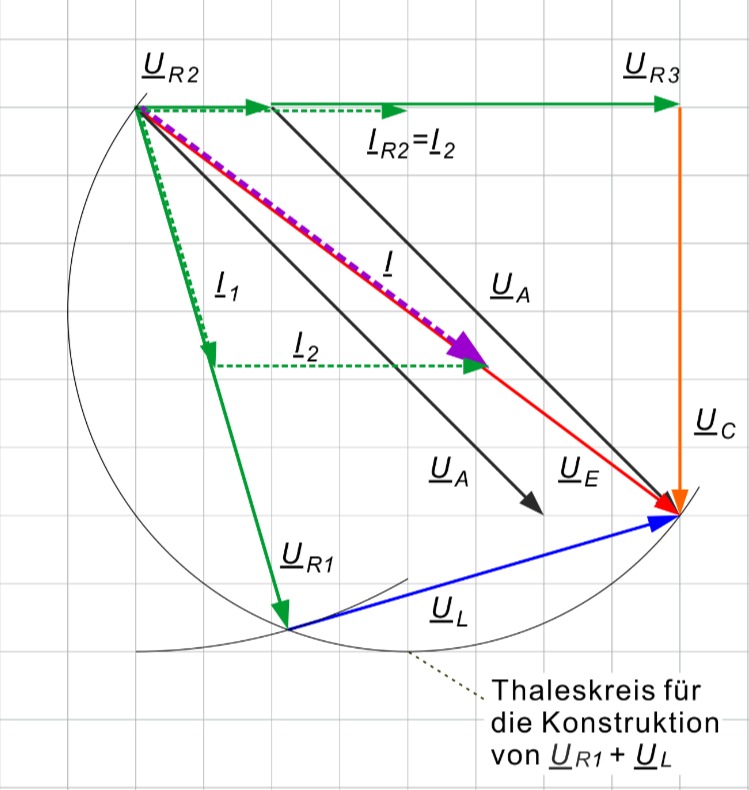
Ergänzung zur Aufgabenstellung
Mit einfacher komplexer Berechnung lässt sich zeigen, dass
Auf einen Hauptnenner bringen:
Da voraussetzungsgemäß die beiden Blindwiderstände gleich sind
Damit wird
Lösung:
siehe Lösungsweg