Aufgabenstellung:
Gegeben ist folgende Schaltungsanordnung:

a) Zeichnen Sie das maßstäbliche Zeigerdiagramm für alle Ströme und Spannungen bei der Frequenz
Beginnen Sie die Zeichnung mit der Spannung
Tragen Sie diese nach rechts gerichtet ein.
Die Zeiger für
b) Wie groß ist der Phasenwinkel zwischen
c) Welchen Amplitudenwert hat
d) Welchen Wert muss der Kondensator
Ermitteln Sie den Wert des Kondensators
e) Welchen Wert muss der Kondensator
Ermitteln Sie den Wert des Kondensators
Lösungsweg:
a) Zeigerdiagramm
Berechnung der Blindwiderstände:
Ermittlung der Spannungs- und Strommaßstäbe:
Man wählt (willkürlich):
Mit
Dieser Strom
Der Strom in
Der Betrag ist:
vom Ursprung nach unten abgetragen
Der Strom
Man liest ab (oder errechnet über den Pythagoras) die Länge dieses Zeigers:
Mit dem Strommaßstab erhält man:
Jetzt lässt sich die Spannung über dem Kondensator
mit dem Spannungsmaßstab:
diese Spannung ist gegenüber
diese Spannung ist mit
Mit dem Spannungsmaßstab erhält man:
Diese beiden Spannungen vektoriell zur Spannung
Man liest aus dem Zeigerdiagramm ab:
Länge von
Mit dem Spannungsmaßstab erhält man:
vollständiges Zeigerdiagramm
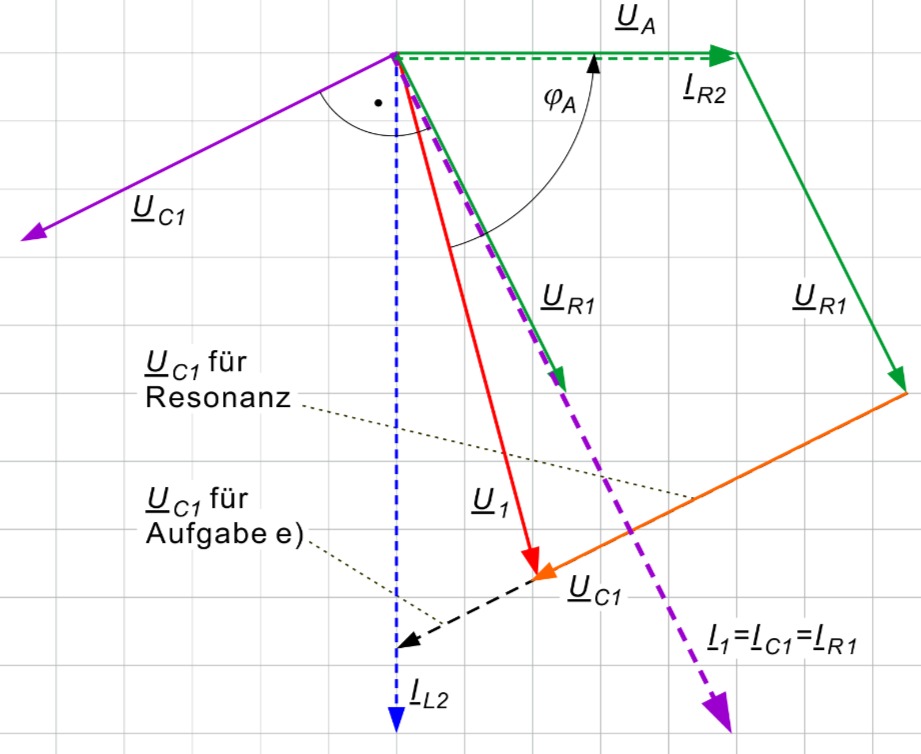
b) Phasenwinkel
ablesen:
Die Spannung
c) Amplitudenwert
Mit
d) Kapazität bei Resonanz
Resonanz:
Aus dem Zeigerdiagramm wird klar, dass die Spannung
Man liest ab: Länge von
mit Spannungsmaßstab:
e) Kapazität
Man liest ab:
Lösung:
siehe Lösungsweg