Aufgabenstellung:
Gegeben ist ein folgendes Zweitor:
Doppel-T-Schaltung
a) Ermitteln Sie die Leitwertmatrix des Zweitors
b) Berechnen Sie die Elemente der Leitwert- und Widerstandsmatrix für den Fall
Hinweis:
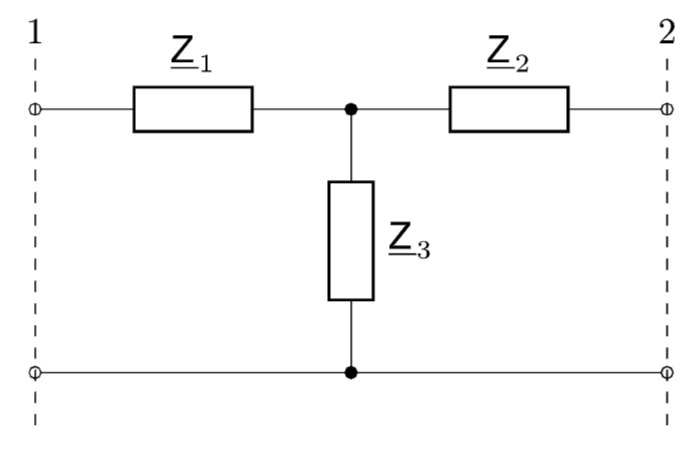
T-Schaltung
Lösungsweg:
a) Leitwertmatrix
Admittanzmatrix mit Hilfe des Verfahrens der Matrixaddition Das gegebene Netzwerk lässt sich
als Parallelschaltung zweier Zweitore darstellen. Die Admittanzmatrix des Gesamtzweitores ist die Summe der Admitanzmatrizen der beiden Teilzweitore. Im folgenden wird anstelle des Widerstandes
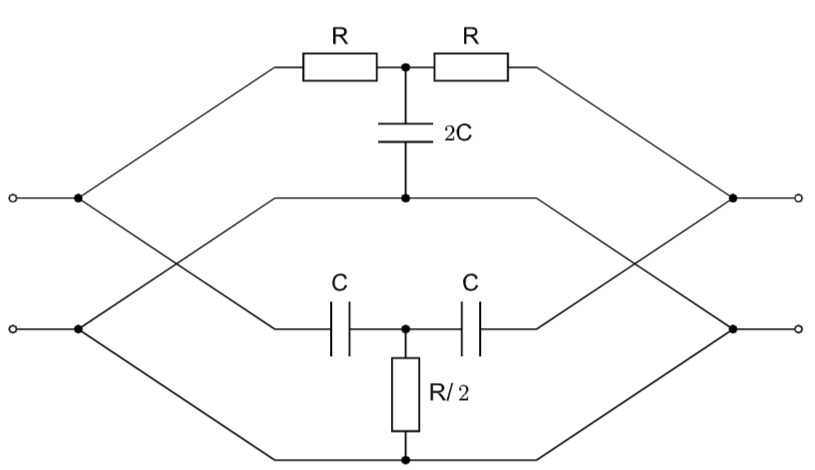
Darstellung des Netzwerkes als Parallelschaltung zweier Zweitore
Die Admitanzmatrix des T-Gliedes ist angegeben. Die Bauelemtewerte im vorliegenden Fall können einfach eingesetzt werden. Es ergibt sich die Admittanzmatrix
Für die Gesamtmatrix
bzw.
b) Leitwert- und Widerstandsmatrix
Für
Für
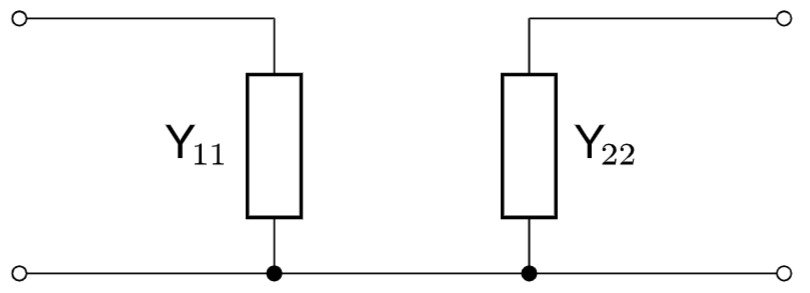
Äquivalentes Zweitor für
Das Netzwerk ist also ein Sperrfilter, das Frequenzanteile um die Kreisfrequenz
Lösung:
a)
b) siehe Lösungsweg