Aufgabenstellung:
Die Scheibe
- Bestimmen Sie die Einspannmomente
und - Wie groß ist die Verdrehung
der Scheibe ? - Ermitteln Sie die maximalen Schubspannungen
und in den Wellen und
Gegeben:
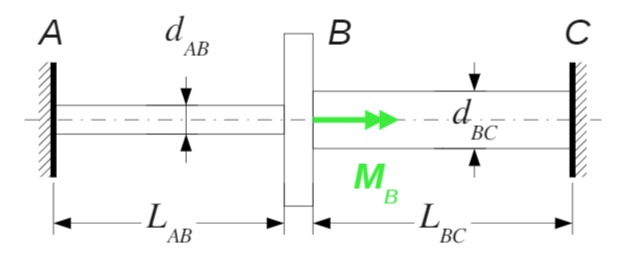
Lösungsweg:
a) Einspannmomente
Balken freischneiden und Momentengleichgewichte aufstellen:
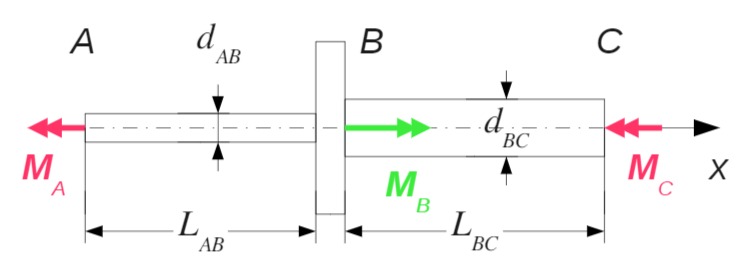
Das System ist einfach statisch unbestimmt, da die Wellen in den Enden
Verlauf des Torsionsmoments:
Abschnitt
Abschnitt
Einsetzen in die Verträglichkeitsbedingung ergibt:
Einsetzen in das Momentengleichgewicht führt auf
Stelle die Gleichungen für die Torsionsträgheitsmomente auf:
Somit folgt als Gleichung für
Zahlenwerte einsetzen:
b) Verdrehung der Scheibe
Die Verdrehung der Scheibe
Zahlenwerte einsetzen:
Über eine Probe kann das Ergebnis (optional) validiert werden:
c) Schubspannungen
Torsionsmomente
Mit den Torsionswiderstandsmomenten berechnet sich die maximalen Schubspannungen zu:
Zahlenwerte einsetzen:
