Aufgabenstellung:
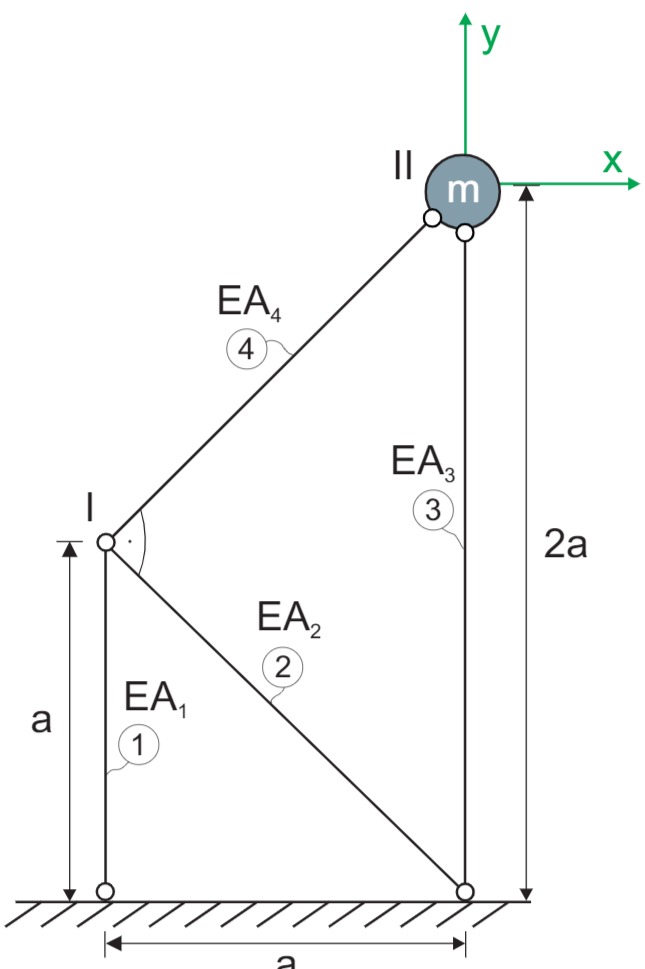 Gegeben ist das dargestellte ungedämpfte ebene Stabwerk, das mit einer Punktmasse
Gegeben ist das dargestellte ungedämpfte ebene Stabwerk, das mit einer Punktmasse
- Geben Sie die Gesamtsteifigkeitsmatrix
und die Massenmatrix unter Vernachlässigung aller Stabmassen an - Berechnen Sie die Eigenfrequenzen des Systems.
Gegeben:
Lösungsweg:
a) Gesamtsteifigkeitsmatrix
Freikörperbild
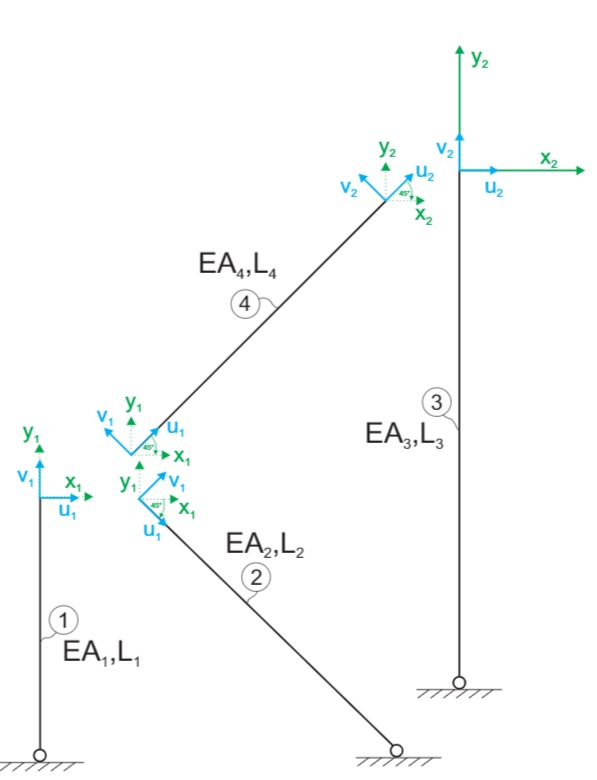 Die grünen Koordinatensysteme sind die globalen Koordinaten
Die grünen Koordinatensysteme sind die globalen Koordinaten
Die lokalen Koordinatensysteme für die Lagerungen wurden hier aufgrund fehlender Verschiebung bereits weg gelassen.
Stab 1
Lokale Steifigkeitsmatrix
Stab 3
Lokale Steifigkeitsmatrix
Stab 2
Das lokale Koordinaten System
Transformationsmatrix:
Lokale Steifigkeitsmatrix
mit
Globale Steifigkeitsmatrix:
Stab 4
Im Gegensatz zu den Stäben
Teil-Transformationsmatrizen:
Transformationsmatrix:
lokale Steifigkeitsmatrix:
Globale Steifigkeitsmatrix:
Die Gesamtsteifigkeitsmatrix
Dafür müssen
Die globale Massenmatrix lautet
Da die Massenmatrix zwei Nullzeilen enthält, kann aus den entsprechenden Zeilen der Steifigkeitsmatrix
Mit diesen Gleichungen in die beiden unteren Spalten von
b) Eigenfrequenzen des Systems
Die Bewegungsgleichung des Massepunktes in
Die Eigenfrequenzen und Eigenvektoren können aus der Lösung des Eigenwertproblems bestimmt werden
Daraus folgt das charakteristische Polynom
mit den Eigenfrequenzen