18 / 38

Aufgabenstellung:

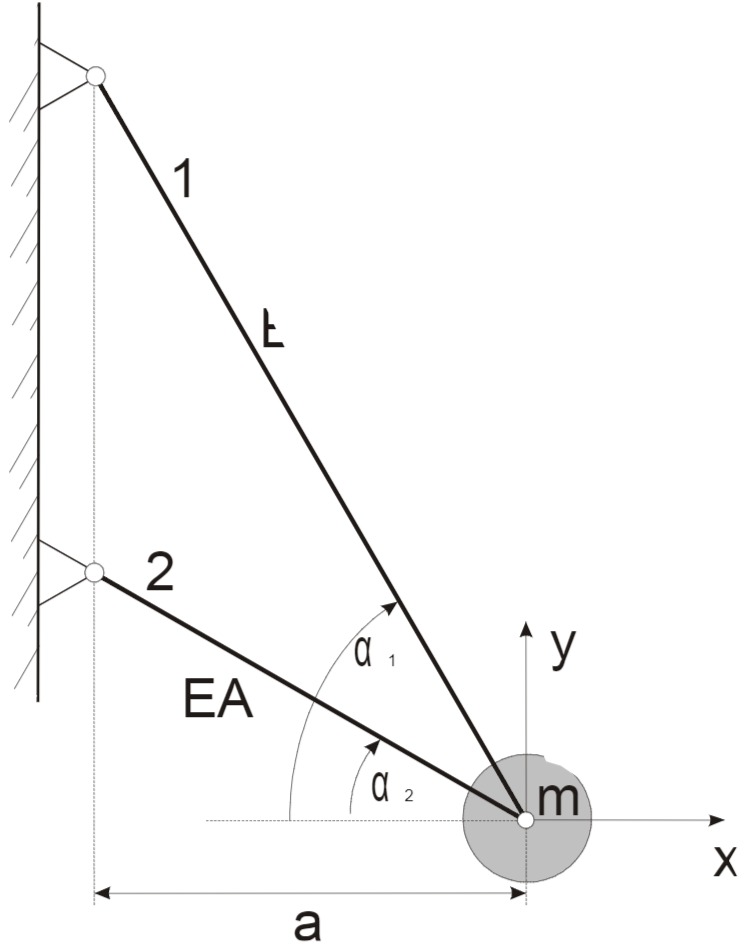AbbildungEine Punktmasse ist an zwei Stäben (EA) gelenkig befestigt Die Geometrie des Stabzweischlages ist der Skizze zu entnehmen

  1. Berechnen Sie die Eigenfrequenzen des Systems für und
  2. Wie lautet die Gleichung zur Bestimmung der Eigenvektoren des Systems?

Gegeben:

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

Zur Berechnung der Steifigkeit des Systems werden zunächst die Verschiebungen des Zweischlages aufgrund von normierten Kräften und bestimmt.

Ermitteln der Stablängen:

Länge des Stabes 1 :

Länge des Stabes 2 :

Bestimmung der Stabkräfte mit :

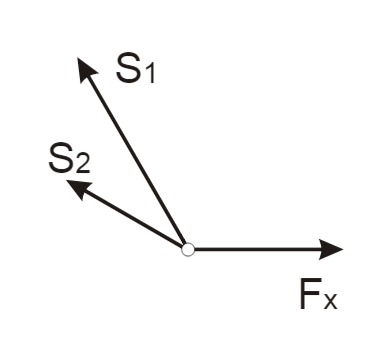
Abbildung

Bestimmung der Stabkräfte mit :

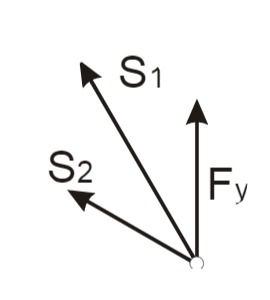
Abbildung

Die Verlängerung der Stäbe ergibt sich mit zu:

Verschiebung in -Richtung aufgrund von

Verschiebung in -Richtung aufgrund von

Verschiebung in -Richtung aufgrund von

Verschiebung in -Richtung aufgrund von

Mit dem hookschen Gesetz gilt .

Diese Werte werden zur Inversen der Steifigkeitsmatrix C zusammengefasst:

Durch Inversion von erhält man

Damit ergibt sich die Bewegungsgleichung zu:

a) Eigenfrequenzen

Die Eigenfrequenzen werden durch die Lösung des Eigenwertproblems ermittelt:

Es ergibt sich das charakteristische Polynom:

Damit ergeben sich die Eigenfrequenzen zu

b) Zur Bestimmung der Eigenvektoren muss folgende Gleichung nach aufgelöst werden:

Lösung: