Aufgabenstellung:
Der zylindrische Halbkörper aus der Abbildung besteht aus zwei Hälften mit unterschiedlicher elektrischer Leitfähigkeit
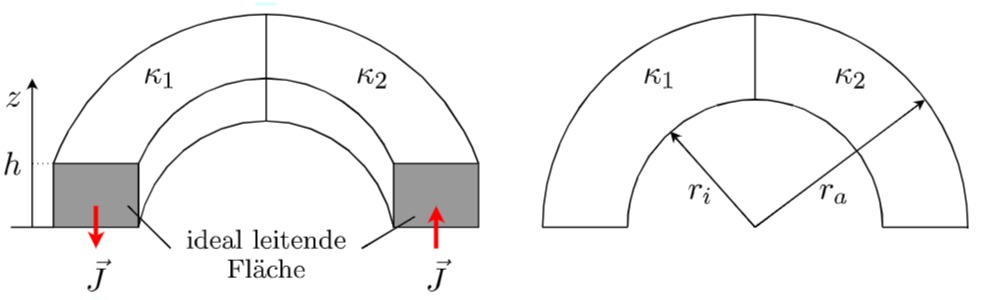
a) Zeichnen Sie das elektrische Ersatzschaltbild mit diskreten Widerständen und tragen Sie alle relevanten elektrischen Größen (Spannung, Strom) ein.
b) Geben Sie die Verhältnisse zwischen den elektrischen Feldstärken
c) Berechnen Sie die elektrischen Feldstärken
d) Gesucht ist der elektrische Strom
Lösungsweg:
a) Ersatzschaltbild
Gesucht: Elektrisches Ersatzschaltbild der Anordnung
Gegeben: Der Strom I fließt durch beide Abschnitte.
Es handelt sich daher um eine Reihenschaltung von zwei Widerständen.
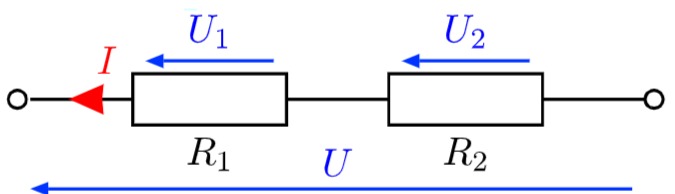
b) Verhältnisse
Gesucht:
Ergänzung: Man beachte das Verhalten der Feldgrößen an Grenzflächen.
Die Gleichgewichtsbedingungen
Aufgrund der Reihenschaltung (gleicher Strom) und der identischen Abmessungen der beiden Abschnitte muss gelten:
c) Feldstärken
Gesucht:
Beim Anlegen einer Spannung U an einen Körper gilt:
Im Ersatzschaltbild sieht man dass die Gesamtspannung sich auf die beiden Widerstände der Abschnitte aufteilt.
Die Feldlinien laufen senkrecht zum Radius
Da die elektrischen Feldlinien außen länger sind als innen, ist die Feldstärke abhängig vom Radius
Sie ist nicht vom Winkel
Da
Da der Intergretionsweg der Feldstärke entlang der Feldlinien verläuft (siehe folgende Abbildung). zeigt das Linienelement ebenfalls nur in Richtung
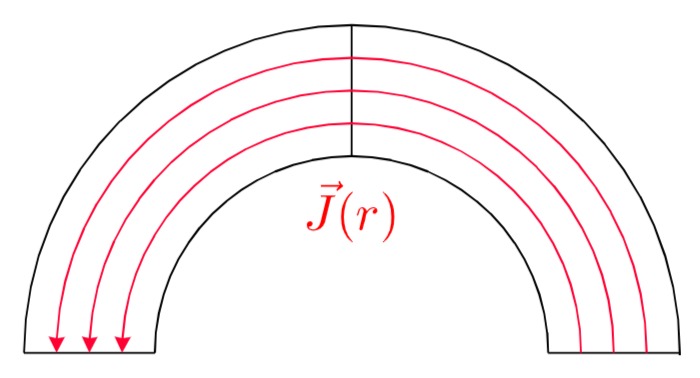
Verlauf der Stromdichte
Das allgemeine Linienelement in Zylinderkoordinaten ist:
nur in Richtung
Es ergibt sich daher:
Die Lösung des Integrals führt auf
Die fehlende Beziehung zur Spannung
Damit ergeben sich die gesuchten elektrischen Feldstärken in den beiden Abschnitten zu
d) Strom
Gesucht: Der elektrische Strom
Gegeben: Leitfähigkeit
Der Strom
Das Flächenelement kann man aus folgender Abbildung ableiten.
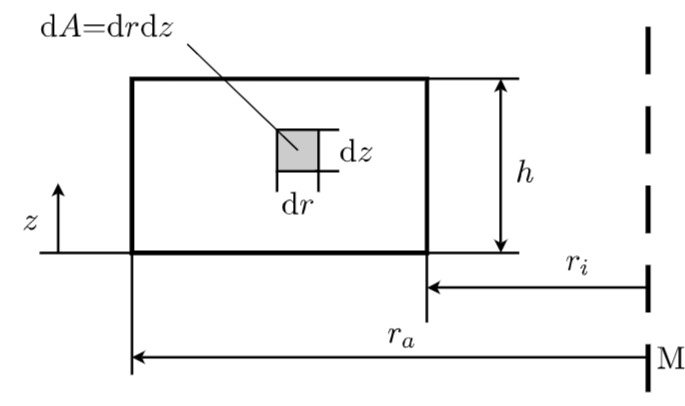
Grafik zur Parametrisierung der Seitenfläche
Einsetzen der Stromdichte
mit der Lösung des Flächenintegrals
Lösung:
siehe Lösungsweg