Aufgabenstellung:
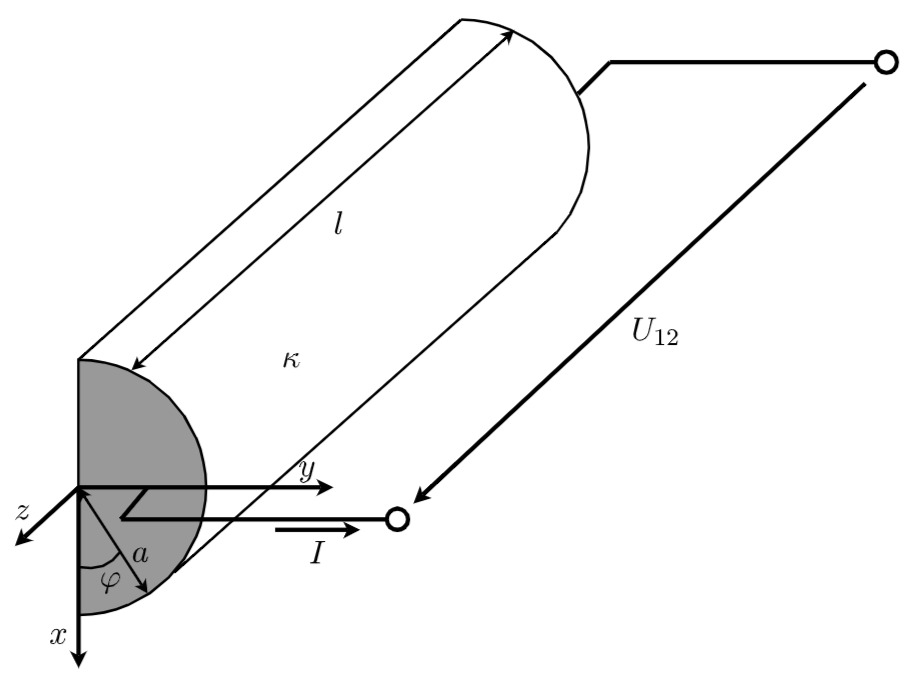
Gegeben sei der in der Abbildung dargestellte Halbzylinder mit der Länge
a) Bestimmen Sie die elektrische Feldstärke
Es gelte nun
b) Bestimmen Sie die Stromdichte
c) Berechnen Sie nun den in
d) Berechnen Sie den Widerstand
Lösungsweg:
a) Elektrische Feldstärke
Die Spannung lässtz sich aus der Feldstärke berechnen nach:
Daraus lässt sich für die Feldstärke angeben:
Die Richtung ist in
b) Stromdichte
Die Stromdichte berechnet sich über die Materialkonstante:
Für den Fall der winkelabhängigen Leitfähigkeit ergibt sich
c) Strom
Die Stromstärke ist das Intergral der Stromdichte über die Fläche, hier also
d) Widerstand
Der Widerstand ist der Quotient aus Spannung und Stromstärke:
Lösung:
sieh Lösungsweg junge