Aufgabenstellung:
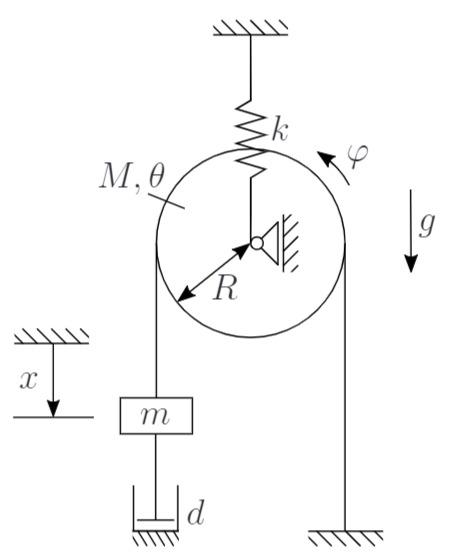
Eine reibungsfrei gelagerte Rolle (Masse
- Bestimmen Sie die Bewegungsgleichung des Systems in der Koordinate
mit der Methode nach LAGRANGE. - Ermitteln Sie die statische Ruhelage
des Systems. - Für die allgemeine Bewegung des Systems in Form einer gedämpften Schwingung bestimme man die Eigenkreisfrequenz
und das Lehr'sche Dämpfungsmaß .
Gegeben:
Hinweis: Andere Lösungswege als die Methode nach LAGRANGE werden hier nicht aufgeführt.
Lösungsweg:
a) Bewegungsgleichung nach Lagrange:
Wichtig: Bewegt sich die Masse
Skizze

Kinematik:
Kinetische Energie:
Potentielle Energie:
Generalisierte Kräfte (Nicht-Potentialkräfte):
Lagrange'sche Gleichung:
Bewegungsgleichung:
b) Statische Ruhelage
c) Eigenkreisfrequenz